Расстояние от точки до плоскости. Уравнение плоскости, проходящей через три заданные точки.

А1(х1,у1,z1), А2(х2,у2,z2), А3(х3,у3,z3):

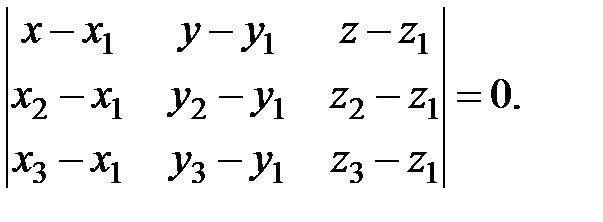
Что представляет собой это уравнение? Имеются три точки А1, А2, А3. Рассмотрим текущую точку плоскости. Ее координаты – переменные А(х,у,z). Все эти четыре точки лежат в одной плоскости, следовательно, и связывающие их вектора лежат в той же самой плоскости. Если три вектора лежат в одной плоскости, они компланарны, а, если вектора компланарны, то объем призмы, построенной на них равен 0. Именно эту формулу смешанного произведения векторов и представляет собой левая часть нашего уравнения плоскости, проходящей через три известные точки А1, А2, А3.

Расстояние от точки до плоскости. Расстояние d от точки М(х1, у1, z1) до плоскости Ах+Вy+Сz+D=0 равно

Не нашли, что искали? Воспользуйтесь поиском: