Множества, операции над множествами.

Множество - это совокупность, набор элементов, объединенных общими свойствами.

Множества обозначаются заглавными латинскими буквами , а элементы множества строчными латинскими буквами .

Запись означает, что есть множество с элементами , которые связаны между собой какой-то функцией .

Замечание. Элементы в множество входят по одному разу, т.е. без повторений.

Основные операции:

Принадлежность элемента множеству:

где -- элемент и -- множество (элемент принадлежит множеству ).

Непринадлежность элемента множеству:

где -- элемент и -- множество (элемент не принадлежит множеству ).

Объединение множеств: .

Объединением двух множеств и называется множество 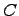, которое состоит из элементов множеств и , т.е.

или

Пересечение множеств: .

Пересечением двух множеств и называется множество 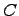, которое состоит из общих элементов множеств и , т.е.

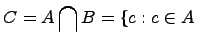и

Разность множеств: .

Разностью двух множеств и , например, множество минус множество , называется множество 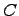, которое состоит из элементов множества , которых нет в множестве , т.е.

и

Симметрическая разность множеств: .

Симметрической разностью двух множеств и называется множество 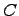, которое состоит из не общих элементов множеств и , т.е.

Дополнение множества: .

Если предположим, что множество является подмножеством некоторого универсального множества , тогда определяется операция дополнения:

и

Вхождение одного множества в другое множество: .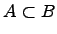

Если любой элемент множества является элементом множества , то говорят, что множество есть подмножество множества (множество входит в множество ).

Не вхождение одного множества в другое множество: .

Если существует элемент множества , который не является элементом множества , то говорят, что множество не подмножество множества (множество не входит в множество ).

Не нашли, что искали? Воспользуйтесь поиском: