Числовая последовательность и ее предел. Ограниченность сходящейся последовательности.

Опр. 1. Последовательностью называется числовая функция f(n), заданная на множестве натуральных чисел N.

Если n — натуральное число, а аn - значение последовательности в точке n, то говорят, что n называется номером числа аn, а само число аn называют общим или n-м членом последовательности. Для последовательности с общим членом аn употребляются следующие обозначения: аn, n=1, 2, …, или {an}.

Опр. 2. Последовательность {an} называется постоянной, если an=с для любого 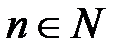, где с – некоторое действительное число ().

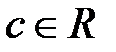Опр. 3. Последовательность {an} называется ограниченной, если найдется число М такое, что |аn|≤ М для всех .

Опр. 4. Последовательность {an} называется возрастающей (убывающей), если an≤an+1 (an≥an+1) для любого . Возрастающие и убывающие последовательности называются монотонными последовательностями.

Опр. 5. Последовательность {an} называется строго возрастающей (строго убывающей), если an<an+1 (an>an+1) для любого . Строго возрастающие и строго убывающие последовательности называются строго монотонными последовательностями.

Опр. 6. Число а называется пределом числовой последовательности {аn}, если для любого, даже сколь угодно малого положительного числа 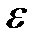>0, найдется такое число N (зависящее от 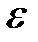, N=N()), что для всех членов последовательности с номерами n>N верно неравенство |аn – а|< . Если это выполняется, то пишут

Теорема 1. Если последовательность ограничена и монотонна, то она сходится.

Теорема 2. Пусть дана постоянная числовая последовательность {an}, где an = с = const для любого 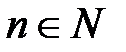. Тогда она сходится и 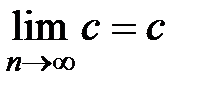(предел постоянной равен постоянной).

Теорема 3. Последовательность {an} с общим членом an= 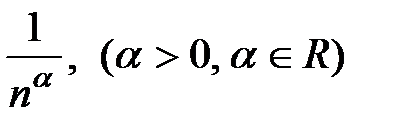сходится и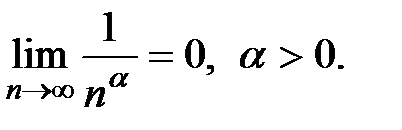

Теорема 4. Если |q| < 1 (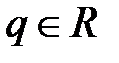), то последовательность {qn} сходится и

Бесконечно малые последовательности и их свойства. (Теорема о сумме двух бесконечно малых последовательностей, теорема о произведении бесконечно малой последовательности на ограниченную последовательность).

Бесконечно малой величиной называется величина, предел которой равен нулю.

Основные свойства бесконечно малых величин:

1. Сумма двух бесконечно малых величин есть величина бесконечно малая.

2. Произведение ограниченной величины на бесконечно малую величину есть бесконечно малая величина. В частности, произведение постоянной величины на величину бесконечно малую, а также произведение бесконечно малых величин есть бесконечно малая величина.

3. Частное от деления бесконечно малой величины на переменную величину, стремящуюся к пределу, не равному нулю, есть бесконечно малая величина.

Не нашли, что искали? Воспользуйтесь поиском: