Односторонние пределы. Непрерывность функции в точке. Классификация точек разрыва. Свойства функций, непрерывных на отрезке.

Опр. 1. Если любая последовательность хn→а, хn<а (а–число или символ -∞) при любом , то говорят, что функция f(x) при х→а-0 (слева) имеет левый односторонний предел Говорят, что функция f(x) при хn→а+0 (справа) имеет правый односторонний предел если функция f(х) была определена правее точки а, и любая последовательность хn→а, хn>а (а–число или символ +∞) при любом .

Если f(х) имеет в точке а (а – число) односторонние пределы f(a-0) и f(a+0) и f(a-0)=f(a+0)=b (b – число или один из символов - ∞ или + ∞), тогда f(x) имеет в точке а обычный (двусторонний) предел Если односторонние пределы различны, т.е. f(a-0)≠f(a+0), то не существует предела функции при х→а.

Опр. 1. Функция f(x) называется непрерывной в точке а, если функция имеет конечный предел в точке а и этот предел совпадает со значением функции в этой точке, т. е.

Опр. 2. Функция называется непрерывной на промежутке X, если она непрерывна в каждой точке этого промежутка.

Теорема 1. Основные элементарные функции непрерывны в областях их определения.

Пусть функция b1 – левосторонний предел функции f(x) в точке х=а, b2 – правосторонний предел функции f(x) в точке х=а. Рассмотрим функцию у=f(x), определенную на интервале X, кроме, быть может, точки 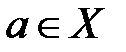. Точка а называется точкой разрыва данной функции, если в ней функция определена, но не является непрерывной, или не определена в этой точке.

В зависимости от характера поведения функции в окрестности точки разрыва различают три основных вида разрывов.

Опр. 1. Точка а называется точкой устранимого разрыва функции f(x), если существует конечный 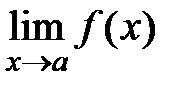, но либо функция не определена в точке а, либо

Опр. 2. Разрыв I рода – в этом случае существуют конечные пределы и , но Величина |b2–b1| называется скачком.

Опр. 3. Разрыв II рода — в этом случае хотя бы один из пределов и не существует или бесконечен.

Не нашли, что искали? Воспользуйтесь поиском: