Каноническое уравнение прямой в пространстве. Уравнение прямой, проходящей через две заданные точки.

Пусть М1(x1, y1, z1) – точка, лежащая на прямой l, и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы 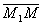и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t. Действительно, из параметрических уравнений почем или .

Угол между двумя прямыми в пространстве. Условие параллельности и перпендикулярности прямых. Угол между прямой и плоскостью. Условие параллельности и перпендикулярности прямой и плоскости.

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

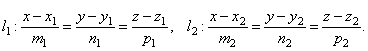
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

.

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов и :

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда параллелен .

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

Рассмотрим векторы и . Если угол между ними острый, то он будет , где φ – угол между прямой и плоскостью. Тогда .

Если угол между векторами и тупой, то он равен . Следовательно . Поэтому в любом случае . Вспомнив формулу вычисления косинуса угла между векторами, получим .

Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой и нормальный вектор плоскости коллинеарны, т.е. .

Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы и перпендикулярны.

Не нашли, что искали? Воспользуйтесь поиском: