Радианная мера угла

Угол в 1 радиан - это такой центральный угол, длина дуги которого равна радиусу окружности (см рисунок ниже). Радианная и градусная меры угла связаны между собой отношением: 180^о= &pi радиан, а угол n^о равен π*n/180 радиан.

Радианная мера угла позволяет упростить некоторые формулы. Например, для окружности радиуса r длина ее дуги l в α радиан вычисляется по формуле: l = α*r. Площать S сектора круга радиуса r, дуга которого содержит α радиан, равна: S=αr²/2. Эти и другие преимущества привели к тому, что в тригонометрии обычно пользуются только радианной мерой угла.

До сих пор, говоря о тригонометрических функциях, мы считали, что аргументами этих функций являются углы или дуги. Теперь мы хотим ввести в рассмотрение тригонометрические функции числового аргумента. Такое желание вполне естественно. Когда мы говорим, например, о квадратной функции у = а х 2, то под х понимаем просто число. Это число может характеризовать время в свободном падении тел (S= gt2/2 ), сопротивление электрической цепи в законе Джоуля — Ленца (Q = IR2) и т. д. Почему же в таком случае, говоря, например, о функции у = tg x, мы под х должны понимать обязательно угол?

Определение. Синусом числа х называется число, равное синусу угла в х радианов. Косинусом числа х называется число, равное косинусу угла в х радианов.

Аналогично определяются и другие тригонометрические функции числового аргумента х. Например, и т. д. Здесь уже π/4, π/3 и π/6 не углы, выраженные в радианах, а просто числа.

№ 14

Основные тригонометрические тождества

• sin² α + cos² α = 1
• tg α · ctg α = 1
• tg α = sin α ÷ cos α
• ctg α = cos α ÷ sin α
• 1 + tg² α = 1 ÷ cos² α
• 1 + ctg² α = 1 ÷ sin² α

№ 15 Функция y = sinx, ee свойства и график

Функция синус y = sin(x).

Изобразим график функции синус, его называют "синусоида".

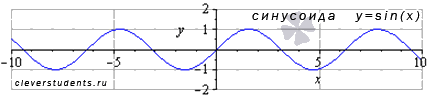
Свойства функции синус y = sinx.

• Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при .
• Наименьший положительный период функции синуса равен двум пи: .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть .
• Функция синус - нечетная, так как .
• Функция убывает при ,
  
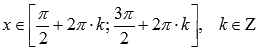  возрастает при .
• Функция синус имеет локальные максимумы в точках ,
  локальные минимумы в точках .
• Функция y = sinx вогнутая при ,
  выпуклая при .
• Координаты точек перегиба .
• Асимптот нет.

№ 16

Функция косинус y = cos(x).

График функции косинус (его называют "косинусоида") имеет вид:

Свойства функции косинус y = cosx.

• Область определения функции косинус: .
• Наименьший положительный период функции y = cosx равен двум пи: .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Область значений функции косинус представляет интервал от минус единицы до единицы включительно: .
• Функция косинус - четная, так как .
• Функция убывает при ,
  возрастает при .
• Функция y = cosx имеет локальные максимумы в точках ,
  локальные минимумы в точках .
• Функция вогнутая при ,
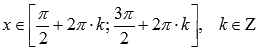  выпуклая при .
• Координаты точек перегиба .
• Асимптот нет.

№ 17

Функция тангенс y = tg(x).

График функции тангенс (его называют "тангенсоида") имеет вид:

Свойства функции тангенс y = tgx.

• Область определения функции тангенс: , где , Z – множество целых чисел.
  Поведение функции y = tgx на границе области определения
  Следовательно, прямые , где , являются вертикальными асимптотами.
• Наименьший положительный период функции тангенс .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Область значений функции y = tgx: .
• Функция тангенс - нечетная, так как .
• Функция возрастает при .
• Функция вогнутая при ,
  
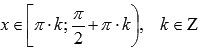  выпуклая при .
• Координаты точек перегиба .
• Наклонных и горизонтальных асимптот нет.

№ 18

Свойства функции котангенс y = ctgx.

• Область определения функции котангенс: 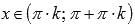, где , Z – множество целых чисел.
  Поведение на границе области определения
  Следовательно, прямые , где являются вертикальными асимптотами.
• Наименьший положительный период функции y = ctgx равен пи: .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Область значений функции котангенс: .
• Функция нечетная, так как .
• Функция y = ctgx убывает при .
• Функция котангенс вогнутая при ,
  выпуклая при .
• Координаты точек перегиба .
• Наклонных и горизонтальных асимптот нет.

№ 19

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

• аркси́нус (обозначение: arcsin)
• аркко́синус (обозначение: arccos)
• аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
• арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
• арксе́канс (обозначение: arcsec)
• арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin⁻¹ для арксинуса и т. п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1.

№ 20

ростейшими называются тригонометрические уравнения следующих четырех видов:

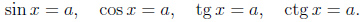
Любое тригонометрическое уравнение в конечном счёте сводится к решению одного или нескольких простейших.

Для решения простейших тригонометрических уравнений мы будем пользоваться тригонометрическим кругом и определениями тригонометрических функций.

Уравнения 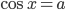, и

— это абсцисса точки на единичной окружности, соответствующей углу .

— это ордината.

Из определения синуса и косинуса следует, что уравнения 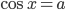и имеют решения только при условии: . Таким образом, уравнения или не имеют решений!

№ 21

Корень

Не нашли, что искали? Воспользуйтесь поиском: