Степень с рациональным показателем

Если:

• a > 0;
• n — натуральное число;
• m — целое число;

Тогда:

Пример 2.

№ 22

Логарифм

[править]

Материал из Википедии — свободной энциклопедии

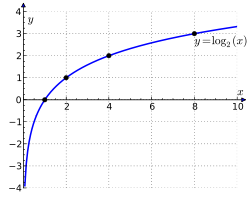
График двоичного логарифма

Логари́фм числа по основанию (от греч. λόγος — «слово», «отношение» и ἀριθμός — «число»^[1]) определяется^[2] какпоказатель степени, в которую надо возвести основание , чтобы получить число . Обозначение: , произносится: " логарифм по основанию ".

Из определения следует, что нахождение равносильно решению уравнения 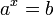. Например, 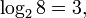потому что

Вычисление логарифма называется логарифмированием. Числа чаще всего вещественные, но существует также теория комплексных логарифмов.

Логарифмы обладают уникальными свойствами, которые определили их широкое использование для существенного упрощения трудоёмких вычислений^[3]. При переходе «в мир логарифмов» умножение заменяется на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня преобразуются соответственно в умножение и деление на показатель степени. Лаплас говорил, что изобретение логарифмов, «сократив труд астронома, удвоило его жизнь»^[4].

Определение логарифмов и таблицу их значений (для тригонометрических функций) впервые опубликовал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, расширенные и уточнённые другими математиками, повсеместно использовались для научных и инженерных расчётов более трёх веков, пока не появились электронные калькуляторы и компьютеры.

Со временем выяснилось, что логарифмическая функция незаменима и во многих других областях человеческой деятельности: решениедифференциальных уравнений, классификация значений величин (например, частота и интенсивность звука), аппроксимация различных зависимостей, теория информации, теория вероятностей и т. д. Эта функция относится к числу элементарных, она обратна по отношению к показательной функции. Чаще всего используются вещественные логарифмы с основанием (натуральный логарифм), (десятичный) и (двоичный).

Свойства

Не нашли, что искали? Воспользуйтесь поиском: