Прямой на плоскости.

1) пусть B≠0, тогда разрешая уравнение относительно y, получим y=-(A/B)x+(-C/B)

положим здесь –A/B=k; -C/B=b.

Тогда y=kx+b.

y

Y M(x; y)

N(O; b) C(x; b)

Α

O x xКаково бы ни было числовое значение –A/B и –C/B всегда найдется такой угол α (0≤α<π,

α≠π/2), что tg α=k=-A/B и точка N на оси Oy, y=b=-C/B.

Итак, (2) определяет прямую.

2) B=0; A≠0, тогда уравнение имеет вид: Ax+C=0; x=-C/A. А это прямая, параллельная

Оси Oy.

3)A=B=0, так как в этом случае уравнение не содержит ни x, ни y, то уравнение (2)

Теряет смысл.

1) A=0, B≠0, By+C=0, y=-C/B – прямая параллельная оси Ox.

Итак, уравнение (2) – это общее уравнение прямой.

Уравнение прямой с угловым коэффициентом.

Пусть на плоскости xOy задана произвольная прямая, не параллельная оси Oy.

Положение этой прямой будем определять следующими двумя параметрами: 1)ординатой точки N пересечения прямой с осью Oy. 2)углом α, который прямая образует с положительным направлением оси Ox. Построим вспомогательный треугольник MCN, в котором катет NC=x, CM=y-b. Из треугольника: CM=NC⋅tg α, то есть y-b=x⋅tg α (1) Введем обозначения tg α=k; k – угловой коэффициент прямой. Из (1) получим y=kx+b – это уравнение прямой с угловым коэффициентом. Если прямая проходит через начало координат, то b=0 и уравнение y=kx Если прямая параллельна оси Ox, то α=0 и уравнение y=b. Уравнение прямой, параллельной оси Oy, получается особо. Ясно, что оно: x=a

Уравнение прямой в каноническом виде

Рассмотрим в пространстве произвольную прямую. Отметим на ней точку, определяющую радиус, вектор и лежащий на ней вектор, приложенный к точке. Произвольную текущую точку прямой обозначим через и ее радиус-вектор через. Вектор можно записать в виде, где - некоторое число (скаляр). Если действительная переменная пробегает интервал, то конец вектора пробегает всю прямую.

.

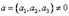
Вопрос 20

Не нашли, что искали? Воспользуйтесь поиском: