Элементы теории графов

Нестрого под графом будем понимать множество точек и соединяющих эти точки линий со стрелками или без них.

Первой работой в теории графов принято считать статью Эйлера (1736 г.), в которой приведены знаменитые рассуждения о Кёнингсбергских мостах. Эйлер доказал, что нельзя обойти семь городских мостов и вернуться в исходное положение, проходя по каждому мосту ровно один раз. Однако на протяжении 100 лет эта работа оставалась единственным достижением теории графов и следующий этап в ее развитии связан с развитием исследований по электрическим сетям, кристаллографии и другим наукам.

В повседневной жизни мы сталкиваемся с графами постоянно. Например, схему линий метрополитена можно рассматривать как граф. Точками на ней представлены станции, а линиями — пути движения поездов. Графы служат удобным средством описания связей между различными объектами. Методы теории графов широко применяются в дискретной математике, в биологии, в химии, в теории вероятностей. В настоящее время теория графов охватывает большой материал и активно развивается. При изложении этой теории ограничимся только частью результатов и основной акцент сделаем на описании графов и обосновании некоторых алгоритмов анализа.

Основные понятия и определения

Рассмотрим произвольное множество и некоторый фиксированный набор , состоящий из пар . Графом называется пара объектов 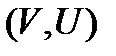, при этом множество называется вершинами, а - ребрами графа . Если множество конечное, то граф называется конечным графом, в противном случае граф называется бесконечным. Каждое ребро графа представимо в ви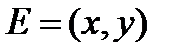де , где и называются концами ребра . Если в представлении ребра 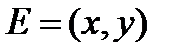не принимается во внимание порядок расположения его концов, т.е. если , то ребро называется неориентированным ребром. 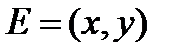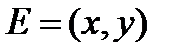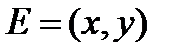Если же в представлении порядок расположения концов существенен, то ребро называется ориентированным ребром или дугой, при этом первую вершину в записи ребра будем называть начальной, а вторую - конечной вершиной. Ребро вида называется петлей. Будем говорить, что ориентированное ребро 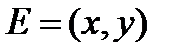является выходящим из вершины и входящим в вершину . называется неориентированным графом (сокращенно: неорграфом), если все его ребра не ориентированы, и ориентированным графом (сокращенно: орграфом), если все его ребра ориентированы. Смешанным графом называется граф, имеющий как ориентированные, так и не ориентированные ребра. Вершины, соединенные ребром или дугой называются смежными. Ребра, имеющие общую вершину, также называются смежными. Независимо от того ориентировано или не ориентировано ребро 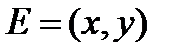, говорят, что оно инцидентно вершинам и , а сами вершины и инцидентны . На рисунках вершины графа обычно обозначают точками (или кружками), а инцидентные им ребра – кривыми, соединяющими эти точки (или кружки).

Если ребро 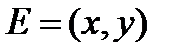ориентировано, то и представляющая его кривая ориентирована в направлении от к . На рис. изображен неориентированный и ориентированный графы.

Поскольку расположение вершин и форма ребер при изображении графа не существенны, то один и тот же граф может представляться различными рисунками. Говорят, что два графа и изоморфны, если между их вершинами и можно установить взаимно однозначное соответствие, при котором вершины в одном графе соединены ребром тогда и только тогда, когда соответствующие им вершины во втором графе так же соединены ребром (причем, если ребра ориентированы, то их направления должны соответствовать друг другу). Вершину, не принадлежащую никакому ребру графа, будем называть изолированной. Граф, имеющий только изолированные вершины, называется нуль-графом. Полным графом называется граф, в котором любые две различные вершины соединены ребром.

Ребра (дуги), соответствующие одним и тем же парам (упорядоченным парам) вершин называются кратными. Граф, не содержащий кратных ребер (дуг) называется простым графом, иначе – мультиграфом. Будем граф называть конечным, если конечны число его вершин и ребер, и бесконечным – в противном случае (т.е. когда граф имеет бесконечное число вершин или ребер). Ясно, что простой граф конечен, если конечно число его вершин. Мультиграф, имеющий конечное число вершин, может быть бесконечным.

Не нашли, что искали? Воспользуйтесь поиском: