Гамильтоновы неорграфы

Пусть - неориентированный граф.

Напомним, что простой цепью называется цепь, которая не содержит повторяющихся вершин, а простым циклом – цикл, не содержащий повторяющихся вершин (кроме совпадающих по определению его концов).

Простая цепь называется гамильтоновой цепью, если она проходит через все вершины графа. Простой цикл называется гамильтоновым циклом, если он проходит через все вершины графа. Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом. Граф, обладающий гамильтоновой цепью и не являющийся гамильтоновым графом, называется полугамильтоновым графом.

Несмотря на внешнее сходство определений эйлеровых и гамильтоновых графов, теории этих понятий имеют мало общего. Так критерий эйлеровости графа был установлен достаточно просто (см. теорему 4). Необходимого и достаточного же условия гамильтоновости графа до настоящего времени не найдено. Однако, существует целый ряд достаточных условий.

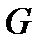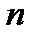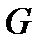Теорема (Оре). Если у графа с вершинами выполнено неравенство для любой пары несмежных вершин , то – гамильтонов граф.

Из этой теоремы вытекает

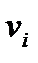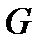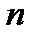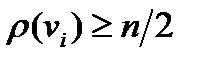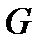Теорема (Дирак). Если для всех вершин графа , имеющего вершин, выполнено неравенство , то – гамильтонов граф.

Эйлеровы орграфы

Рассмотрим ориентированный граф (орграф) . Определение эйлерова ориентированного графа сходно с определением неориентированного эйлерова графа. Предварительно введем вспомогательные понятия. Каркасным графом (коротко: каркасом) для ориентированного графа называется граф, получаемый из снятием направлений всех его дуг. Ориентированный орграф называется слабосвязным (коротко: связным), если связен соответствующий ему каркасный граф. Ориентированная эйлерова цепь это ориентированная цепь, содержащая каждую дугу графа точно один раз. Орграф называется полуэйлеровым, если в нем существует ориентированный эйлерова цепь. Аналогично ориентированная эйлеров цикл это ориентированный цикл, содержащий каждую дугу графа точно один раз. Орграф называется эйлеровым, если в нем существует ориентированный эйлеров цикл.

Аналогично теореме 4 можно доказать следующее утверждение.

Теорема 6. Ориентированный граф , у которого связен соответствующий скелетный граф, является эйлеровым тогда и только тогда когда для любой вершины графа число входящих ребер равно числу исходящих ребер, т.е. равны полустепени захода и исхода вершины :

.

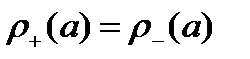Теорема 7. Ориентированный граф , у которого связен соответствующий скелетный граф, является полуэйлеровым тогда и только тогда когда существует в точности две вершины 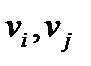, такие что

,

а для остальных вершин

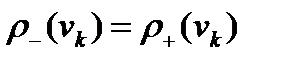
(в этом случае эйлерова цепь начинается в вершине , а заканчивается в вершине ).

Вопросы, связанные с распознаванием гамильтоновости (полугамильтоновости) графа и построение соответствующих гамильтоновых циклов (цепей) являляются достаточно сложными и мы на них не будем останавливаться.

Не нашли, что искали? Воспользуйтесь поиском: