
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Кратчайшие пути. Алгоритм Дейкстры.
До сих пор нами рассматривались графы и составляющие их вершины и ребра (дуги), по которым можно перемещаться. Рассмотрим сейчас не только перемещение из одной вершины в другую, но и то, как это сделать наилучшим способом, выбранным в соответствии с каким-либо критерием. Рассмотрим критерии, базирующиеся на понятии веса ребра (дуги) графа. Для этого присвоим каждому ребру или дуге графа определенный вес. Соображения, по которым присваивается тот или иной вес, могут быть различными и зависят от существа решаемой задачи. Например, если в качестве вершин графа выбираются города, а в качестве дуг – авиалинии между этими городами, то, в зависимости от интересующей нас задачи, весом ребра или дуги  может являться либо длина перелета, либо время перелета, либо стоимость билета из
может являться либо длина перелета, либо время перелета, либо стоимость билета из  в
в  и т.д. Ребра (дуги) графа, которым присвоен некоторый вес, будем называть взвешенными ребрами (дугами). Граф, ребрам или дугам которого присвоен определенный вес, будем называть взвешенным графом. В дальнейшем будем предполагать, что рассматриваемый граф является ориентированным, а вес любой дуги – некоторое неотрицательное число, причем для удобства несуществующим дугам графа присвоим бесконечный вес. Обозначим вес дуги
и т.д. Ребра (дуги) графа, которым присвоен некоторый вес, будем называть взвешенными ребрами (дугами). Граф, ребрам или дугам которого присвоен определенный вес, будем называть взвешенным графом. В дальнейшем будем предполагать, что рассматриваемый граф является ориентированным, а вес любой дуги – некоторое неотрицательное число, причем для удобства несуществующим дугам графа присвоим бесконечный вес. Обозначим вес дуги  через
через  , при этом
, при этом  , если вершины
, если вершины  и
и  не соединены дугой. Будем говорить, что вершина
не соединены дугой. Будем говорить, что вершина  графа достижима из его вершины
графа достижима из его вершины  , если существует связывающий их путь
, если существует связывающий их путь  , составленный из дуг графа, в котором вершина
, составленный из дуг графа, в котором вершина  является начальной, а вершина
является начальной, а вершина  - конечной:
- конечной:
 .
.
Длиной или весом этого пути 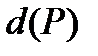 называется сумма длин, входящих в него дуг:
называется сумма длин, входящих в него дуг:
 .
.
Наименьшее значение из длин путей, связывающих вершины  и
и  , назовем расстоянием от
, назовем расстоянием от  до
до  и обозначим
и обозначим  . Если вершина
. Если вершина  не достижима из
не достижима из  , то расстояние от
, то расстояние от  до
до  , обозначаемое тем же символом
, обозначаемое тем же символом  , полагается бесконечным. Путь
, полагается бесконечным. Путь  , длина которого равна расстоянию
, длина которого равна расстоянию  , называется кратчайшим путем. Отметим, что кратчайших путей может быть несколько. Если
, называется кратчайшим путем. Отметим, что кратчайших путей может быть несколько. Если  , то не имеет смысла говорить о кратчайшем пути.
, то не имеет смысла говорить о кратчайшем пути.
Многие задачи сводятся или к нахождению кратчайшего пути или к нахождению расстояния от одной вершины графа до другой его вершины. Рассмотрим один из наиболее известных алгоритмов нахождения расстояния от одной вершины графа до другой - алгоритм Дейкстры (Едсгер Дейкстра, нидерландский математик, 1930 – 2002).
Итак, пусть  – ориентированный граф с взвешенными дугами. Обозначим через
– ориентированный граф с взвешенными дугами. Обозначим через  -вершину – начало пути и через
-вершину – начало пути и через  -вершину – конец пути. Алгоритм Дейкстры представляет собой итерационную процедуру, на каждом шаге которой всем вершинам графа
-вершину – конец пути. Алгоритм Дейкстры представляет собой итерационную процедуру, на каждом шаге которой всем вершинам графа  приписываются числа (метки)
приписываются числа (метки)  , которые служат оценкой длины (веса) кратчайшего пути от вершины
, которые служат оценкой длины (веса) кратчайшего пути от вершины  к вершине
к вершине  . Если вершина
. Если вершина  получила на некотором шаге метку
получила на некотором шаге метку  , то это означает, что в графе
, то это означает, что в графе  найдется путь
найдется путь  из
из  в
в  , имеющий вес
, имеющий вес  . Метки, присваемые вершинам, могут быть временными или постоянными. Превращение метки в постоянную означает, что кратчайшее расстояние от вершины
. Метки, присваемые вершинам, могут быть временными или постоянными. Превращение метки в постоянную означает, что кратчайшее расстояние от вершины  до соответствующей вершины найдено.
до соответствующей вершины найдено.
Перед первой итерацией начальной вершине  присваивается постоянная метка
присваивается постоянная метка  , а все остальные вершины получают временные метки, равные бесконечности. Каждая итерация алгоритма состоит в просматривании меток вершин, к которым ведут дуги из вершины, которая последней получила постоянную метку (для первой итерации это вершина
, а все остальные вершины получают временные метки, равные бесконечности. Каждая итерация алгоритма состоит в просматривании меток вершин, к которым ведут дуги из вершины, которая последней получила постоянную метку (для первой итерации это вершина  ). Пусть
). Пусть  - последняя вершина, которой присвоена постоянная метка. Тогда каждой вершине
- последняя вершина, которой присвоена постоянная метка. Тогда каждой вершине  , не имеющей постоянной метки, присваивается новая временная метка, равная
, не имеющей постоянной метки, присваивается новая временная метка, равная  .
.
Ясно, что нет смысла рассматривать вершины  , к которым не ведут дуги из вершины
, к которым не ведут дуги из вершины  . Для таких вершин
. Для таких вершин  и поэтому
и поэтому
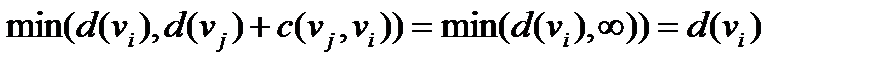 ,
,
т.е. значения меток таких вершин остаются неизменными. Каждая итерация заканчивается выбором из вершин с временными метками вершины, обозначим ее  , с наименьшим значением метки и превращением этой метки в постоянную (если таких вершин несколько, то выбираем любую из них).
, с наименьшим значением метки и превращением этой метки в постоянную (если таких вершин несколько, то выбираем любую из них).
Алгоритм заканчивает работу, когда заданная конечная вершина  получает постоянную метку. Рассмотрим следующий
получает постоянную метку. Рассмотрим следующий
Пример. В графе с взвешенными ребрами найти длину кратчайшего пути от вершины  до вершины
до вершины  .
.
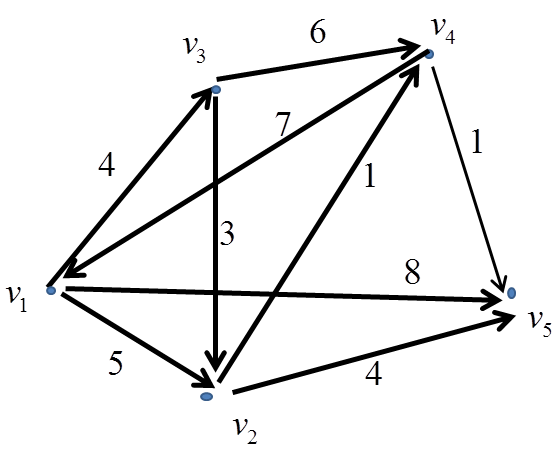
1 шаг. Вершине  присваиваем постоянную метку
присваиваем постоянную метку  остальным вершинам придадим временные бесконечные метки:
остальным вершинам придадим временные бесконечные метки:
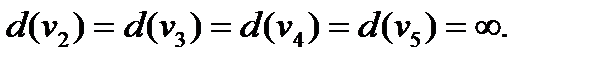
2 шаг. Пересчитываем метки вершин, являющихся концами дуг, выходящих из вершины с последней постоянной меткой, т.е. из вершины  . При этом временные метки остальных вершин оставим без изменения. Получим
. При этом временные метки остальных вершин оставим без изменения. Получим
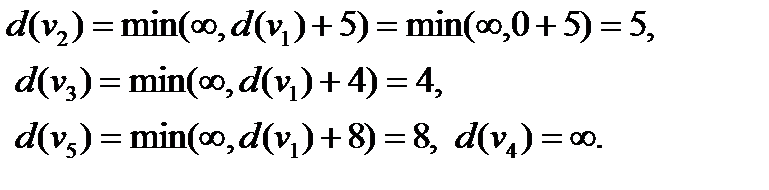
Выбираем из этих меток наименьшую:  и превратим ее в постоянную.
и превратим ее в постоянную.
3 шаг. Пересчитываем метки вершин, не имеющих постоянных меток и являющихся концами дуг, выходящих из вершины с последней постоянной меткой, т.е. из вершины  . При этом вновь временные метки остальных вершин оставим без изменения. Получим
. При этом вновь временные метки остальных вершин оставим без изменения. Получим
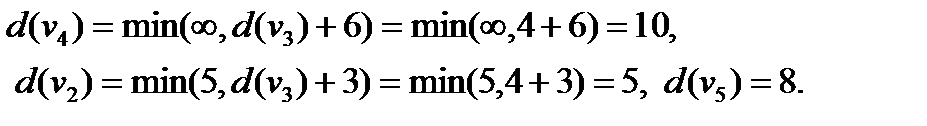
Выбираем из этих меток наименьшую:  и превращаем ее в постоянную метку.
и превращаем ее в постоянную метку.
4 шаг. Пересчитываем метки вершин, не имеющих постоянных меток и являющихся концами дуг, выходящих из вершины с последней постоянной меткой, т.е. из вершины  . При этом, как и ранее, временные метки остальных вершин оставляем без изменения. Имеем:
. При этом, как и ранее, временные метки остальных вершин оставляем без изменения. Имеем:
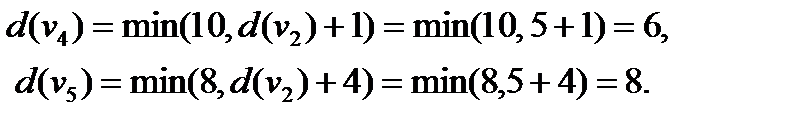
Выбираем из этих меток наименьшую:  и превращаем ее в постоянную метку. Вершина
и превращаем ее в постоянную метку. Вершина 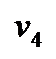 получила постоянную метку
получила постоянную метку  . Таким образом, длина кратчайшего пути от вершины
. Таким образом, длина кратчайшего пути от вершины  до вершины
до вершины  (или, что то же самое, расстояние от вершины
(или, что то же самое, расстояние от вершины  до вершины
до вершины  ) равно 6. Нетрудно видеть, что путь
) равно 6. Нетрудно видеть, что путь 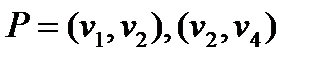 и является кратчайшим путем.
и является кратчайшим путем.
Работа алгоритма показана в следующей таблице. Постоянные метки вершин заключены в квадратные скобки.
| Вершина\ Итерация | 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| ||
| ----- | 
| 
| ||||
| ----- | 
| ----- | ||||
| ----- | ----- | ----- | 
| |||
КОНТРОЛЬНАЯ РАБОТА
1 ЗАДАНИЕ. Для графа  с заданными мощностями
с заданными мощностями  (т.е.
(т.е.  -число вершин, а
-число вершин, а 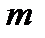 - число ребер графа) составьте матрицы смежности и инцидентности. Определите локальные степени вершин. Является ли граф, соответствующий Вашему варианту эйлеровым, полуэйлеровым, гамильтоновым и почему?
- число ребер графа) составьте матрицы смежности и инцидентности. Определите локальные степени вершин. Является ли граф, соответствующий Вашему варианту эйлеровым, полуэйлеровым, гамильтоновым и почему?
| n | ||||||||||
| m |
2 ЗАДАНИЕ. Найдите эйлерову цепь в графах.
3 ЗАДАНИЕ. Найти расстояние от вершины  до вершины
до вершины  и построить соответствующий кратчайший маршрут.
и построить соответствующий кратчайший маршрут.
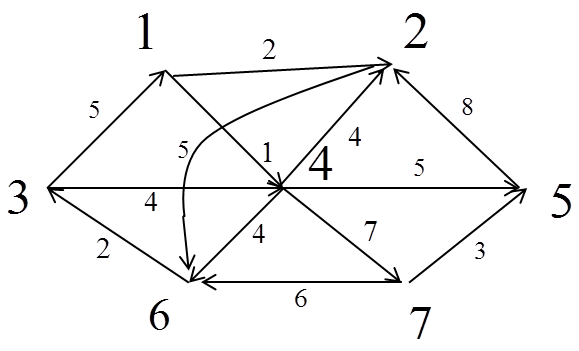
| 1 вар. | 2 вар. | 3 вар. | 4 вар. | 5 вар. |
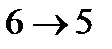
| 
| 
| 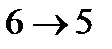
| 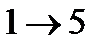
|
| 6 вар. | 7 вар. | 8 вар. | 9 вар. | 10 вар. |

| 
| 
| 
| 
|
Не нашли, что искали? Воспользуйтесь поиском: