Маршруты, цепи, циклы. Связность графов

Рассмотрим неориентированный граф . Маршрутом в называется любая последовательность ребер

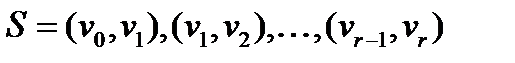. (2)

Вершины 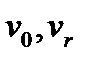называются концами маршрута . Будем говорить, что есть маршрут длины , соединяющий вершины и 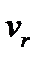. Для любых двух вершин 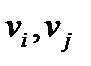маршрута 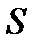подмаршрут

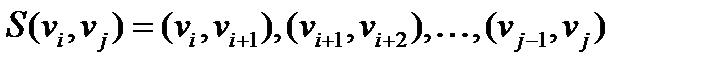
будем называть участком .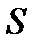

При определении маршрута не накладывается никаких ограничений на повторяемость входящих в него ребер, вершин. Каждое такое ограничение будет отражено в последующих определениях. Маршрут 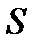называется замкнутым, если в нем совпадают начальная и конечная вершины: Не замкнутый маршрут называется цепью, если в нем нет повторяющихся ребер (при этом вершины в цепи могут повторяться). Простой цепью называется цепь, которая не содержит повторяющихся вершин. Замкнутый маршрут, не содержащий повторяющихся ребер, называется циклом. Цикл, не содержащий повторяющихся вершин (кроме совпадающих по определению его концов), называется простым циклом.

До сих пор мы предполагали, что граф неориентированный. Все выше сформулированные определения (маршрута, цепи, простой цепи, цикла) переносятся и на ориентированные графы. При этом, в определении в определении маршрута

надо потребовать, что бы его составляли дуги. Такой маршрут в дальнейшем иногда будем называть путем.

Пусть - неориентированный граф. Граф 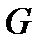называется связным, если любые две его вершины можно соединить цепью, в противном случае граф называется несвязным. Отношение связности позволяет произвести разложение всех вершин графа

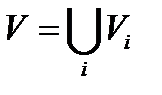(3)

на непересекающиеся подмножества вершин так, что все вершины внутри каждого связаны, а вершины из различных не связаны между собой. Равенство (3) влечет разложение графа

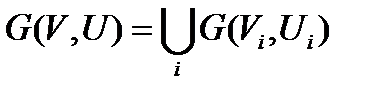(4)

на непересекающиеся связные подграфы 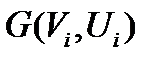, которые называются связными компонентами графа 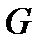. Таким образом, нами получена следующая

Теорема 2. Произвольный неориентированный граф единственным образом разлагается в прямую сумму связных компонент.

Эта теорема позволяет, в частности, позволяет свести изучение несвязных неориентированных графов к изучению связных графов. Из теоремы 1 вытекает

Теорема 3. Если ровно две вершины графа имеют нечетную степень, то они связаны.

Обозначим через 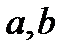вершины, имеющие нечетные степени, и пусть вершина принадлежит связной компоненте 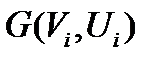в разложении (4). По теореме 1 в конечном неориентированном графе число вершин нечетной степени четно. Поэтому, применяя эту теорему к графу 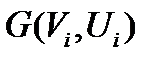, получим, что и вершина принадлежит этой же компоненте 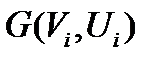. А это означает, что вершины и связаны.

Эйлеровы неорграфы

Рассмотрим вновь неориентированный граф . Напомним, что незамкнутый маршрут называется цепью, если в нем нет повторяющихся ребер. Цепь, содержащая все ребра графа 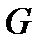, называется эйлеровой цепью, а граф, содержащий такую цепь, называется полуэйлеровым графом. Напомним так же, что замкнутый маршрут, не содержащий повторяющихся ребер, называется циклом. Цикл, содержащий все ребра графа 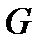, называется эйлеровым циклом, а граф, содержащий такой цикл, называется эйлеровым графом.

Теорема 4. Конечный граф 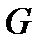является эйлеровым тогда и только тогда, когда

1) граф 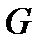связен; 2) все степени его вершин четны.

Доказательство. Пусть 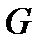является эйлеровым графом. Условие 1), очевидно, является необходимым. Для доказательства необходимости условия 2) заметим, что при всяком прохождении эйлерова цикла через любую вершину графа используется одно ребро для входа и одно ребро для выхода. Поскольку каждое ребро используется один раз, то каждая вершина должна иметь четную степень.

Докажем достаточность условий 1), 2). Допустим, что эти условия выполнены. Начнем строить цепь обхода ребер графа из произвольной его вершины и будем продолжать ее все время, насколько это возможно, через новые (ранее не встречавшиеся) ребра. Так как все вершины имеют четную степень, то этот процесс построения может закончиться только в вершине . Обозначим построенный цикл через . Если цикл содержит все ребра графа 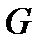, то - эйлеров цикл и достаточность условий 1), 2) доказана. Допустим, что цикл не содержит все ребра графа 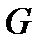. Тогда удалим из 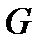все ребра цикла . Оставшийся граф обозначим через 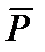. Так как вершины графов и 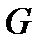имеют четные степени, то и степени всех вершин оставшегося графа 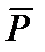так же четные. Так как граф 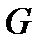связен, то в графе обязательно найдется вершина, инцидентная ребрам графа 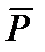. Обозначим эту вершину . Из вершины вновь начнем строить цепь, обходя только ребра из 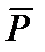. Как и ранее, такая цепь может закончиться только в вершине . Обозначим вновь построенный цикл . Из циклов и образуем новый цикл

,

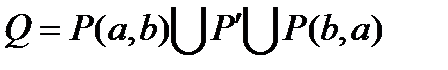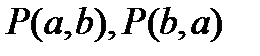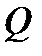где - подмаршруты, составляющие . Если цикл содержит все ребра графа 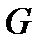, то - эйлеров цикл и достаточность условий 1), 2) доказана. В противном случае построение продолжается. Так как граф 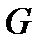конечный, то процесс построения заканчивается и эйлеров цикл будет построен.

Аналогично теореме 4 доказывается

Теорема 5. Конечный граф 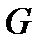является полуэйлеровым тогда и только тогда, когда

1) граф 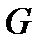связен; 2) ровно две его вершины имеют нечетные степени.

Отметим, что эйлерова цепь в теореме 5 выходит из одной вершины с нечетной степенью и входит в другую вершину с нечетной степенью.

Не нашли, что искали? Воспользуйтесь поиском: