
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ТЕМЫ КОНТРОЛЬНЫХ РАБОТ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ. Далее приведены варианты контрольной работы
ПО ИХ ВЫПОЛНЕНИЮ.
I семестр
ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ
Далее приведены варианты контрольной работы. Отметим, что номер варианта контрольной работы, выполняемой студентом, должен совпадать с последней цифрой номера его зачетной книжки.
Вариант 0.
1. Найти пределы функций (не применяя правила Лопиталя)
1. 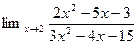 4.
4. 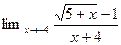
2. 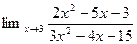 5.
5. 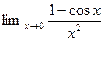
3. 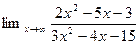
2. Вычислить производную функций
1. 
2. 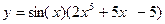
Вычислить 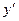 в точке x = 5, если
в точке x = 5, если 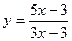
Найти экстремумы функции 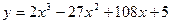
Найти наибольшее и наименьшее значение функции 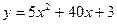 на отрезке [0; 7]
на отрезке [0; 7]
Вычислить 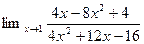
 , используя правило Лопиталя
, используя правило Лопиталя
3. Вычислить следующие интегралы:
1. 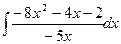
2. 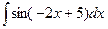
3. 
4. 
4. 1) Имеются 12 единиц товара в одинаковых упаковках. Известно, что в четырех из них товар первого сорта. Случайным образом отбирают 3 единицы товара. Вычислить вероятность того, что среди них:
а) только упаковки с товаром первого сорта;
б) ровно одна упаковка с товаром первого сорта.
2) В магазин поступила обувь от двух поставщиков. Количество обуви, поступившей от первого поставщика, в 2 раза больше, чем от второго. Известно, что в среднем 20% обуви от первого поставщика и 35% обуви от второго поставщика имеют различные дефекты отделки. Из общей массы наугад отбирают одну упаковку с обувью. Оказалось, что она не имеет дефекта отделки. Какова вероятность, что её изготовил первый поставщик?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0, 01 | p | 0, 23 | 0, 28 | 0, 19 | 0, 11 | 0, 06 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
Вариант 1.
1. Найти пределы функций (не применяя правила Лопиталя)
1. 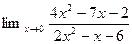 4.
4. 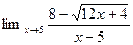
2.  5.
5. 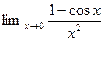
3. 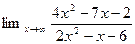
2. Вычислить производную функций
1.
1. 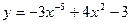
2. 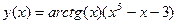
2. Вычислить 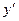 в точке x = -5, если
в точке x = -5, если 
3. Найти экстремумы функции 
4. Найти наибольшее и наименьшее значение функции 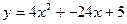 на отрезке [2;5]
на отрезке [2;5]
5. Вычислить 
 , используя правило Лопиталя
, используя правило Лопиталя
3. Вычислить следующие интегралы:
1. 
2. 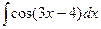
3. 
4. 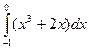
4. 1. В коробке 25 одинаковых по форме шоколадных конфет. Известно, что 15 штук из них сорта «Мишка на Севере», а остальные — сорта «Красная Шапочка». Случайным образом выбирают 3 конфеты. Вычислите вероятность того, что среди них: а) все конфеты сорта «Мишка на севере»; б) только одна конфета этого сорта.
2. В магазин поступил одноименный товар, изготовленный двумя предприятиями. С первого предприятия поступило 150 единиц, из них 30 единиц первого сорта, а со второго предприятия 200 единиц, из них 50 первого сорта. Из общей массы товара наугад извлекается одна единица. Какова вероятность того, что она изготовлена на первом предприятии?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0, 2 | 0, 31 | 0, 24 | p | 0, 07 | 0, 04 | 0, 01 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
Вариант 2.
1. Найти пределы функций (не применяя правила Лопиталя)
1. 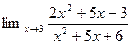 4.
4. 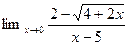
2. 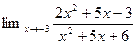 5.
5. 
3. 
2. Вычислить производную функций
1.
1. 
2. 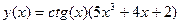
2. Вычислить 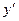 в точке x = 2, если
в точке x = 2, если 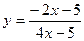
3. Найти экстремумы функции 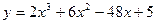
4. Найти наибольшее и наименьшее значение функции  на отрезке [-6;-3]
на отрезке [-6;-3]
5. Вычислить 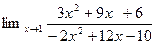
 , используя правило Лопиталя
, используя правило Лопиталя
3. Вычислить следующие интегралы:
1. 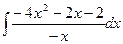
2. 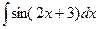
3. 
4. 
4. 1. В туристической группе 15 человек, среди которых только 5 человек хорошо говорят по - английски. В Лондоне группу случайным образом расселили в два отеля (3 человека и 12 человек соответственно). Вычислить вероятность того, что из членов группы в первом отеле: а) все туристы хорошо говорят по - английски; б) только один турист хорошо говорит по - английски.
2. Покупатель может приобрести нужный ему товар в двух магазинах. Вероятности обращения в каждый из двух магазинов зависят от их местоположения и соответственно равны 0,3 и 0,7. Вероятность того, что к приходу покупателя нужный ему товар не будет распродан, равна 0,8 для первого магазина и 0,4 для второго. Какова вероятность того, что покупатель приобретет нужный ему товар?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0, 04 | 0, 08 | 0, 32 | 0, 31 | 0, 15 | 0, 08 | p |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
Вариант 3.
1. Найти пределы функций (не применяя правила Лопиталя)
1. 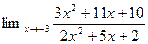 4.
4. 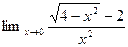
2.  5.
5. 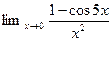
3. 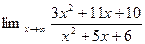
2. Вычислить производную функций
1.
1. 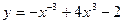
2. 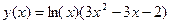
2. Вычислить 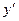 в точке x = 0, если
в точке x = 0, если 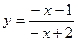
3. Найти экстремумы функции 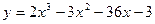
4. Найти наибольшее и наименьшее значение функции  на отрезке [-6;-3]
на отрезке [-6;-3]
5. Вычислить 
 , используя правило Лопиталя
, используя правило Лопиталя
3. Вычислить следующие интегралы:
1. 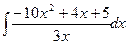
2. 
3. 
4. 
4. 1. В упаковке 12 одинаковых книг. Известно, что каждая третья книга имеет дефект обложки. Случайным образом выбирают 3 книги. Вычислите вероятность того, что среди них: а) все книги имеют дефект обложки; б) только одна книга имеет этот дефект.
2. Два контролёра производят оценку качества выпускаемых изделий. Вероятность того, что очередное изделие попадет к первому контролеру, равна 0,55; ко второму контролеру контролеру – 0,45. Первый контролёр выявляет дефект с вероятностью 0,8, а второй – с вероятностью 0,9. Вычислите вероятность того, что изделие с дефектом будет признано годным к эксплуатации.
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,42 | 0,23 | p | 0,10 | 0,06 | 0,03 | 0,01 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
Вариант 4.
1. Найти пределы функций (не применяя правила Лопиталя)
1. 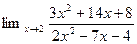 4.
4. 
2.  5.
5. 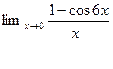
3. 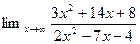
2. Вычислить производную функций
1.
1. 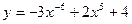
2. 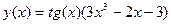
2. Вычислить 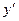 в точке x = -5, если
в точке x = -5, если 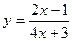
3. Найти экстремумы функции 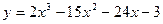
4. Найти наибольшее и наименьшее значение функции  на отрезке [-6;-1]
на отрезке [-6;-1]
5. Вычислить 
 , используя правило Лопиталя
, используя правило Лопиталя
3. Вычислить следующие интегралы:
1. 
2. 
3. 
4. 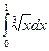
4. 1. К экзамену приготовлено 24 одинаковых ручки. Известно, что треть из них имеет фиолетовый стержень, остальные – синий стержень. Случайным образом отбирают три ручки. Вычислить вероятность того, что:
а) все ручки имеют фиолетовый стержень; б) только одна ручка имеет фиолетовый стержень.
2. Пассажир может приобрести билет в одной из двух касс. Вероятность обращения в первую кассу составляет 0,4, а во вторую – 0,6. Вероятность того, что к моменту приход пассажира нужные ему билеты будут распроданы, равна 0,35 для первой кассы и 0,7 для второй. Пассажир посетил одну из касс и приобрел билет. Какова вероятность того, что он приобрел его во второй кассе?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | p | 0,29 | 0,12 | 0,15 | 0,21 | 0,16 | 0,04 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
Вариант 5.
1. Найти пределы функций (не применяя правила Лопиталя)
1. 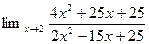 4.
4. 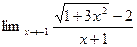
2. 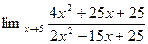 5.
5. 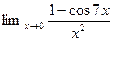
3. 
2. Вычислить производную функций
1.
1. 
2. 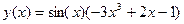
2. Вычислить 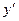 в точке x = 3, если
в точке x = 3, если 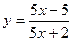
3. Найти экстремумы функции 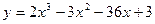
4. Найти наибольшее и наименьшее значение функции 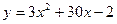 на отрезке [-6;-2]
на отрезке [-6;-2]
5. Вычислить 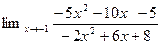
 , используя правило Лопиталя
, используя правило Лопиталя
3. Вычислить следующие интегралы:
1. 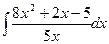
2. 
3. 
4. 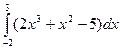
4. 1.В нижней палате парламента 40 депутатов, среди которых первая партия имеет 20 представителей, вторая – 12 представителей, третья 5 представителей, а остальные считают себя независимыми. Случайным образом выбирают трех депутатов. Вычислите вероятность того, что среди них:
а) только представители первой партии, б) только один депутат из первой партии.
2.Два специалиста ОТК проверяют качество выпускаемых изделий, причем каждое изделие с одинаковой вероятностью может быть проверено любым из них. Вероятность выявления дефекта первым специалистом равна 0,8, а вторым 0,9. Из массы проверенных изделий наугад выбрано одно, оно оказалось с дефектом. Какова вероятность того, что ошибку допустил второй контролер?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,05 | 0,12 | 0,18 | 0,30 | p | 0,12 | 0,05 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
Вариант 6.
1. Найти пределы функций (не применяя правила Лопиталя)
1. 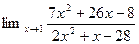 4.
4. 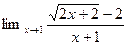
2. 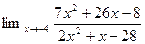 5.
5. 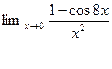
3. 
2. Вычислить производную функций
1.
1. 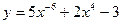
2. 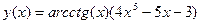
2. Вычислить 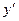 в точке x = 5, если
в точке x = 5, если 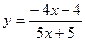
3. Найти экстремумы функции 
4. Найти наибольшее и наименьшее значение функции  на отрезке [2;9]
на отрезке [2;9]
5. Вычислить 
 , используя правило Лопиталя
, используя правило Лопиталя
3. Вычислить следующие интегралы:
1. 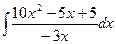
2. 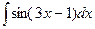
3. 
4. 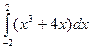
4. 1. В ящике 18 одинаковых бутылок пива без этикеток. Известно, что треть из них «Жигулевское». Случайным образом выбирают 3 бутылки. Вычислите вероятность того, что среди них: а) только пиво сорта «Жигулевское»; б) ровно одна бутылка этого сорта.
2. В двух одинаковых коробках находятся карандаши “Конструктор”. Известно, что треть карандашей в первой коробке и ¼ во второй имеют твердость ТМ. Наугад выбирается коробка, из нее наугад извлекается один карандаш. Он оказывается твердости ТМ. Какова вероятность того, что он извлечен из первой коробки?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,16 | 0,25 | 0,25 | 0,16 | 0,10 | p | 0,03 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
Вариант 7.
1. Найти пределы функций (не применяя правила Лопиталя)
1. 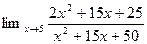 4.
4. 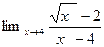
2. 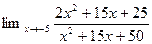 5.
5. 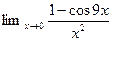
3. 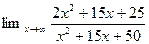
2. Вычислить производную функций
1.
1. 
2. 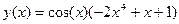
2. Вычислить 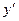 в точке x = 3, если
в точке x = 3, если 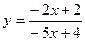
3. Найти экстремумы функции 
4. Найти наибольшее и наименьшее значение функции 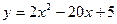 на отрезке [1;8]
на отрезке [1;8]
5. Вычислить 
 , используя правило Лопиталя
, используя правило Лопиталя
3. Вычислить следующие интегралы:
1. 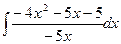
2. 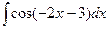
3. 
4. 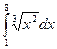
4. 1. В студенческой группе 20 девушек. Известно, что 5 из них не любят читать детективы. Случайным образом выбирают трех девушек и дарят им по детективу. Вычислите вероятность того, что: а) все девушки оценят этот подарок; б) только одна девушка оценит этот подарок.
2. Товаровед плодоовощной базы определяет сорт поступившей от постоянного поставщика партии яблок. Известно. что в среднем 40% выращенного поставщиком урожая составляют яблоки первого сорта. Вероятность того, что товаровед признает первосортную партию первым сортом, равна 0,85. Кроме того, он может допустить ошибку, сочтя непервосортную партию первосортной, с вероятностью 0,2. Какова вероятность того, что он неверно установит сорт партии яблок?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,06 | p | 0,12 | 0,24 | 0,33 | 0,14 | 0,03 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
Вариант 8.
1. Найти пределы функций (не применяя правила Лопиталя)
1. 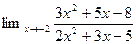 4.
4. 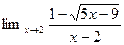
2. 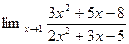 5.
5. 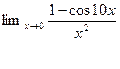
3. 
2. Вычислить производную функций
1.
1. 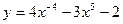
2. 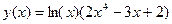
2. Вычислить 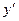 в точке x = -5, если
в точке x = -5, если 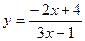
3. Найти экстремумы функции 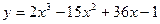
4. Найти наибольшее и наименьшее значение функции 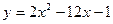 на отрезке [2;6]
на отрезке [2;6]
5. Вычислить 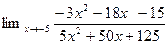
 , используя правило Лопиталя
, используя правило Лопиталя
3. Вычислить следующие интегралы:
1. 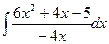
2. 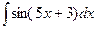
3. 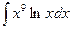
4. 
4. 1. В коробке 30 одинаковых юбилейных монет. Известно, что 5 из них имеют нестандартный процент содержания золота. Случайным образом выбирают три монеты. Вычислите вероятность того, что: а) все монеты имеют нестандартный процент содержания золота; б) только одна монета имеет нестандартный процент содержания золота.
2. М агазин получил две равные по количеству партии одноименного товара. Известно что 25% первой партии и 40% второй партии составляет товар первого сорта. Какова вероятность того, что наугад выбранная единица товара будет не первого сорта?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,02 | 0,38 | 0,30 | p | 0,08 | 0,04 | 0,02 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
Вариант 9.
1. Найти пределы функций (не применяя правила Лопиталя)
1. 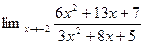 4.
4. 
2. 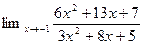 5.
5. 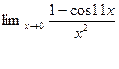
3. 
2. Вычислить производную функций
1.
1. 
2. 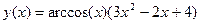
2. Вычислить 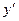 в точке x = 3, если
в точке x = 3, если 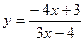
3. Найти экстремумы функции 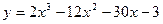
4. Найти наибольшее и наименьшее значение функции 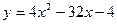 на отрезке [-8;-3]
на отрезке [-8;-3]
5. Вычислить 
 , используя правило Лопиталя
, используя правило Лопиталя
3. Вычислить следующие интегралы:
1. 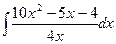
2. 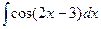
3. 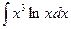
4. 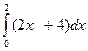
4. 1. На витрине 32 одинаковые булочки. Известно, что среди них четверть булочек с изюмом, остальные с корицей. Случайным образом отбирают три булочки. Вычислите вероятность того, что: а) все выбранные булочки с изюмом; б) только одна булочка с изюмом.
2. Укупорка банок производится двумя автоматами с одинаковой производительностью. Доля банок с дефектом укупорки для первого автомата составляет 1%, а для второго 0,5%. Какова вероятность того, что наугад взятая банка будет иметь дефект укупорки?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,08 | 0,10 | 0,14 | 0,17 | 0,19 | 0,18 | p |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
Семестр.
ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ
Далее приведены варианты контрольной работы. Отметим, что номер варианта контрольной работы, выполняемой студентом, должен совпадать с последней цифрой номера его зачетной книжки.
Вариант 0.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами  ;
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 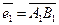 ,
, 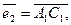
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 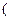
 ,
,
если A1(1, - 1, 0), B1(2, 3, 1), C1(- 1, 1, 1), D1(4, - 3, 5).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы:
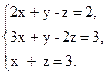
3. Имеются 12 единиц товара в одинаковых упаковках. Известно, что в четырех из них товар первого сорта. Случайным образом отбирают 3 единицы товара. Вычислить вероятность того, что среди них:
а) только упаковки с товаром первого сорта;
б) ровно одна упаковка с товаром первого сорта.
4. В магазин поступила обувь от двух поставщиков. Количество обуви, поступившей от первого поставщика, в 2 раза больше, чем от второго. Известно, что в среднем 20% обуви от первого поставщика и 35% обуви от второго поставщика имеют различные дефекты отделки. Из общей массы наугад отбирают одну упаковку с обувью. Оказалось, что она не имеет дефекта отделки. Какова вероятность, что её изготовил первый поставщик?
6. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0, 01 | p | 0, 23 | 0, 28 | 0, 19 | 0, 11 | 0, 06 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью
y = | x - 1|.
6. Известно, что в среднем 64% студентов потока выполняют контрольные работы в срок. Какова вероятность того, что из 100 студентов потока задержат представление контрольных работ:
а) 30 студентов; б) от 30 до 40 студентов?
Вариант 1.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A 1 B 1;
б) косинус угла между векторами 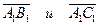 ;
;
в) уравнение ребра A1B1;
г) уравнение грани A 1 B 1 C 1;
д) уравнение высоты, опущенной из вершины D 1 на грань A 1 B 1 C 1;
е) координаты векторов 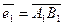 ,
, 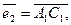
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 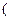
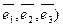 ,
,
если A1(2, 0, - 3), B1(1, 1, 1), C1(4, 6, 6), D1(- 1, 2, 3).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
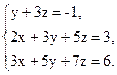
3. В коробке 25 одинаковых по форме шоколадных конфет. Известно, что 15 штук из них сорта «Мишка на Севере», а остальные — сорта «Красная Шапочка». Случайным образом выбирают 3 конфеты. Вычислите вероятность того, что среди них: а) все конфеты сорта «Мишка на севере»; б) только одна конфета этого сорта.
4. В магазин поступил одноименный товар, изготовленный двумя предприятиями. С первого предприятия поступило 150 единиц, из них 30 единиц первого сорта, а со второго предприятия 200 единиц, из них 50 первого сорта. Из общей массы товара наугад извлекается одна единица. Какова вероятность того, что она изготовлена на первом предприятии?
6. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0, 2 | 0, 31 | 0, 24 | p | 0, 07 | 0, 04 | 0, 01 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью
y = 2x + 3.
6. Известно, что в среднем 14% стаканов, изготовляемых на данном предприятии, имеет дефект. Какова вероятность того, что из 300 стаканов данной партии: а) имеют дефект 45; б) не имеют дефекта от 230 до 250.
Вариант 2.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами  ;
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 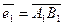 ,
, 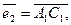
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 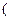
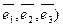 ,
,
если A1(- 3, 1, 1), B1(0, - 4, - 1), C1(5, 1, 3), D1(4, 6, - 2).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.

3. В туристической группе 15 человек, среди которых только 5 человек хорошо говорят по - английски. В Лондоне группу случайным образом расселили в два отеля (3 человека и 12 человек соответственно). Вычислить вероятность того, что из членов группы в первом отеле: а) все туристы хорошо говорят по - английски; б) только один турист хорошо говорит по - английски.
4. Покупатель может приобрести нужный ему товар в двух магазинах. Вероятности обращения в каждый из двух магазинов зависят от их местоположения и соответственно равны 0,3 и 0,7. Вероятность того, что к приходу покупателя нужный ему товар не будет распродан, равна 0,8 для первого магазина и 0,4 для второго. Какова вероятность того, что покупатель приобретет нужный ему товар?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0, 04 | 0, 08 | 0, 32 | 0, 31 | 0, 15 | 0, 08 | p |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = x2 – 1.
6. Установлено, что предприятие бытового обслуживания выполняет в срок в среднем 60% заказов. Какова вероятность того, что из 150 заказов, принятых в течение некоторого времени, будут выполнены в срок:
а) ровно 90 заказов; б) от 93 до 107 заказов.
Вариант 3.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами 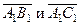 ;
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 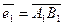 ,
, 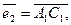
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 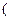
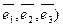 ,
,
если A1(1, 1, 4), B1(2, 1, 2), C1(1, - 1, 2), D1(6, - 3, 8).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
3. В упаковке 12 одинаковых книг. Известно, что каждая третья книга имеет дефект обложки. Случайным образом выбирают 3 книги. Вычислите вероятность того, что среди них: а) все книги имеют дефект обложки; б) только одна книга имеет этот дефект.
4. Два контролёра производят оценку качества выпускаемых изделий. Вероятность того, что очередное изделие попадет к первому контролеру, равна 0,55; ко второму контролеру контролеру – 0,45. Первый контролёр выявляет дефект с вероятностью 0,8, а второй – с вероятностью 0,9. Вычислите вероятность того, что изделие с дефектом будет признано годным к эксплуатации.
6. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,42 | 0,23 | p | 0,10 | 0,06 | 0,03 | 0,01 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = - 2 x + 1.
6. Известно, что в данном технологическом процессе 10% изделий имеют дефект. Какова вероятность того, что в партии из 400 изделий:
а) не будут иметь дефекта 342 изделия;
б) будут иметь дефект от 30 до 52 изделий.
Вариант 4.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами  ;
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 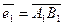 ,
, 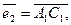
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 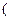
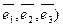 , если
, если
A1(2, 1, - 4), B1(- 3, - 5, 6), C1(0, - 3, - 1), D1(- 5, 2, - 8).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.

3. К экзамену приготовлено 24 одинаковых ручки. Известно, что треть из них имеет фиолетовый стержень, остальные – синий стержень. Случайным образом отбирают три ручки. Вычислить вероятность того, что:
а) все ручки имеют фиолетовый стержень; б) только одна ручка имеет фиолетовый стержень.
4. Пассажир может приобрести билет в одной из двух касс. Вероятность обращения в первую кассу составляет 0,4, а во вторую – 0,6. Вероятность того, что к моменту приходя пасажира нужные ему билеты будут распроданы, равна 0,35 для первой кассы и 0,7 для второй. Пассажир посетил одну из касс и приобрел билет. Какова вероятность того, что он приобрел его во второй кассе?
5. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | p | 0,29 | 0,12 | 0,15 | 0,21 | 0,16 | 0,04 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y = ½ x ½.
6. По данным телеателье установлено, что в среднем 20% цветных телевизоров выходят из строя в течение гарантийного срока. Какова вероятность того, что из 225 проданных цветных телевизоров будут работать исправно в течение гарантийного срока: а) 164 телевизора; б) от 172 до 184 телевизоров.
Вариант 5.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами  ;
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 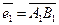 ,
, 
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 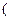
 ,
,
если A1(3, 0, 1), B1(1, 3, 0), C1(4, - 1, 2), D1(- 4, 3, 5).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.

3. В нижней палате парламента 40 депутатов, среди которых первая партия имеет 20 представителей, вторая – 12 представителей, третья 5 представителей, а остальные считают себя независимыми. Случайным образом выбирают трех депутатов. Вычислите вероятность того, что среди них:
а) только представители первой партии, б) только один депутат из первой партии.
4. Два специалиста ОТК проверяют качество выпускаемых изделий, причем каждое изделие с одинаковой вероятностью может быть проверено любым из них. Вероятность выявления дефекта первым специалистом равна 0,8, а вторым 0,9. Из массы проверенных изделий наугад выбрано одно, оно оказалось с дефектом. Какова вероятность того, что ошибку допустил второй контролер?
6. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,05 | 0,12 | 0,18 | 0,30 | p | 0,12 | 0,05 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью y =5x - 2.
6. При оценке качества продукции было установлено, что в среднем третья часть выпускаемой фабрикой обуви имеет различные дефекты отделки. Какова вероятность того, что в партии из 200 пар, поступившей в магазин:
а) будут иметь дефекты отделки 60 пар;
б) не будут иметь дефектов отделки от 120 до 148 пар.
Вариант 6.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами  ;
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 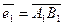 ,
, 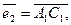
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 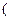
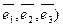 ,
,
если A1(3, 0, - 1), B1(- 1, - 2, - 4), C1(- 1, 2, 4), D1(7, - 3, 1).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.

3. В ящике 18 одинаковых бутылок пива без этикеток. Известно, что треть из них «Жигулевское». Случайным образом выбирают 3 бутылки. Вычислите вероятность того, что среди них: а) только пиво сорта «Жигулевское»; б) ровно одна бутылка этого сорта.
4. В двух одинаковых коробках находятся карандаши “Конструктор”. Известно, что треть карандашей в первой коробке и ¼ во второй имеют твердость ТМ. Наугад выбирается коробка, из нее наугад извлекается один карандаш. Он оказывается твердости ТМ. Какова вероятность того, что он извлечен из первой коробки?
6. Задан закон распределения дискретной случайной величины X:
| X | - 2 | - 1 | |||||
| p | 0,16 | 0,25 | 0,25 | 0,16 | 0,10 | p | 0,03 |
Найти:
а) неизвестную вероятность p;
б) математическое ожидание M, дисперсию D и среднее квадратическое отклонение s данной случайной величины;
в) функцию распределения F(x) и построить её график;
г) закон распределения случайной величины Y, если её значения заданы функциональной зависимостью
y = 4½ x ½ - 1.
6. Известно, что вероятность рождения мальчика равна 0,51, а девочки 0,49. Какова вероятность того, что 300 новорожденных окажется:
а) 150 мальчиков; б) от 150 до 200 мальчиков?
Вариант 7.
1. В декартовой прямоугольной системе координат даны вершины пирамиды A1, B1, C1, D1. Найдите:
а) длину ребра A1B1;
б) косинус угла между векторами  ;
;
в) уравнение ребра A1B1;
г) уравнение грани A1B1C1;
д) уравнение высоты, опущенной из вершины D1 на грань A1B1C1;
е) координаты векторов 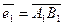 ,
, 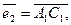
 и докажите, что они образуют линейно независимую систему;
и докажите, что они образуют линейно независимую систему;
ж) координаты вектора  , где M и N – середины ребер A1D1 и B1C1 соответственно;
, где M и N – середины ребер A1D1 и B1C1 соответственно;
з) разложение вектора  по базису
по базису 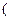
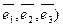 ,
,
если A1(2, - 2, 1), B1(1, 2, - 1), C1(1, 0, 2), D1(2, 1, 0).
2. Решите систему линейных уравнений
а) методом Крамера;
б) методом Гаусса;
в) с помощью обратной матрицы.
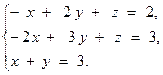
Не нашли, что искали? Воспользуйтесь поиском: