
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Элементы теории вероятности и математической статистики
Для решения задачи 3 см.  глава 1, § 1 – 5.
глава 1, § 1 – 5.
ЗАДАЧА 3.
На складе университета хранится 28 одинаковых упаковок писчей бумаги. Известно, что в четырех из них содержится бумага более низкого качества. Случайным образом выбирают три упаковки бумаги. Вычислить вероятность того, что среди них:
а) нет упаковок с бумагой более низкого качества,
б) есть одна упаковка такой бумаги.
Решение. Общее число возможных элементарных исходов для данных испытаний равно числу способов, которыми можно извлечь 3 упаковки бумаги из 28 упаковок, то есть  – числу сочетаний из 28 элементов по 3.
– числу сочетаний из 28 элементов по 3.
а) Подсчитаем число исходов, благоприятствующих интересующему нас событию (нет упаковок с бумагой более низкого качества). Это число исходов ровно числу способов, которыми можно извлечь 3 упаковки бумаги из 24 упаковок (столько упаковок содержит бумагу высшего сорта), то есть

искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
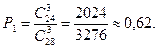
б) Подсчитаем число исходов, благоприятствующих данному событию (среди трех упаковок бумаги ровно 1 упаковка содержит бумагу более низкого качества): две упаковки можно выбрать из 24 упаковок:  способами, при этом одну упаковку нужно выбирать из четырех:
способами, при этом одну упаковку нужно выбирать из четырех: 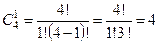 способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно 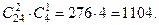
Искомая вероятность равна отношению числа исходов, благоприятствующих данному событию, к числу всех элементарных исходов 
 .
.
Ответ: а)  б)
б) 
ЗАДАЧА 4.
Магазин получает электролампочки с двух заводов, причем доля первого завода составляет 25 %. Известно, что доля брака на этих заводах равна соответственно 5 % и 10 % от всей выпускаемой продукции. Продавец наугад берет одну лампочку. Какова вероятность того, что она окажется бракованной?
Решение: Обозначим через А событие – «лампочка окажется бракованной». Возможны следующие гипотезы о происхождении этой лампочки:  «лампочка поступила с первого завода»,
«лампочка поступила с первого завода»,  «лампочка поступила со второго завода». Так как доля первого завода составляет 25 %, то вероятности этих гипотез равны соответственно
«лампочка поступила со второго завода». Так как доля первого завода составляет 25 %, то вероятности этих гипотез равны соответственно 
Условная вероятность того, что бракованная лампочка выпущена первым заводом –  вторым заводом –
вторым заводом –  искомую вероятность того, что продавец взял бракованную лампочку, находим по формуле полной вероятности
искомую вероятность того, что продавец взял бракованную лампочку, находим по формуле полной вероятности  .
.
Ответ: 
Для решения задачи 5 см.  глава 6 § 1 – 3, глава 7 § 1 – 2, глава 8 § 1 – 3.
глава 6 § 1 – 3, глава 7 § 1 – 2, глава 8 § 1 – 3.
ЗАДАЧА 5.
Задан закон распределения дискретной случайной величены Х:
| Х | – 4 | – 2 | |||||
| р | 0,05 | р | 0,12 | 0,23 | 0,32 | 0,14 | 0,04 |
Найти:
а) неизвестную вероятность р,
б) математическое ожидание М, дисперсию D и среднее квадратическое отклонение  данной случайной величены;
данной случайной величены;
в) функцию распределения F(x) и построить ее график;
г) закон распределения случайной величины Y, если ее значения заданы функциональной зависимостью 
Решение:
а) так как сумма всех вероятностей должна равняться единице, то получим уравнение
 Отсюда
Отсюда 
б) Математическое ожидание М это сумма всех произведений значений случайной величины на их вероятности:

Дисперсия D= 


Среднее квадратическое отклонение  =
= 
в) Если 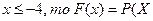 <
< 
Если – 4<  <
< 
Если – 2<  <
< 
Если 0<  0,05 + 0,1 + 0,12 = 0,15 + 0,12 = 0,27
0,05 + 0,1 + 0,12 = 0,15 + 0,12 = 0,27
Если 2<  0,27 + 0,23 = 0,5;
0,27 + 0,23 = 0,5;
Если 4< 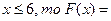 0,5 + 0,32 = 0,82;
0,5 + 0,32 = 0,82;
Если 6<  0,82 + 0,14=0,96;
0,82 + 0,14=0,96;
Если х >8, то F(x)=Р(Х < х)= 0,96 + 0,04=1.
Итак, функция распределения может быть записана так:
 |
F (x) =

График этой функции приведен на рисунке:
г) Сначала найдем значения случайной величены Y.
По условиям задачи 
Поэтому 

Составим таблицу вида.
| Y | – 1 | ||||||
| P | 0,05 | 0,1 | 0,12 | 0,23 | 0,32 | 0,14 | 0,04 |
Чтобы получить закон распределения случайной величены Y необходимо:
1) рассмотреть ее значение в порядке возрастания;
2) сложить вероятности, соответствующие совпадающим значениям данной таблицы.
Итак, закон распределения случайной величены Y:
| Y | – 1 | ||||
| Р | 0,12 | 0,33 | 0,37 | 0,14 | 0,04 |
Для решения задачи 6 см.  глава 5, §2, §3.
глава 5, §2, §3.
ЗАДАЧА 6.
Известно, что вероятность положительного исхода некоторого опыта равна 0,125. Найдите вероятность того, что в серии из 128 опытов положительный исход произойдет
а) в 20 опытах
б) от 12 до 20 опытов.
Решение:
а) воспользуемся локальной теоремой Лапласа. Вероятность того, что в n =128 испытаниях, в каждом из которых вероятность появления события равна  равна к=20 раз (безразлично, в какой последовательности) приближенно равна
равна к=20 раз (безразлично, в какой последовательности) приближенно равна 
Так как 
 то
то 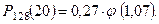
Значение функции  находим в таблице (см. например,
находим в таблице (см. например,  , стр. 461):
, стр. 461): 
Итак, 
Отметим, что таблица функции  приведена только для положительных значений. Если же значение
приведена только для положительных значений. Если же значение  получилось отрицательным, то знак минус можно просто опустить в силу четности функции
получилось отрицательным, то знак минус можно просто опустить в силу четности функции  .
.
б) воспользуемся интегральной теоремой Лапласа. Вероятность того, что в n =128 независимых испытаниях событие наступит от К1=12 до К2 =20 раз приближенно равна

Так как 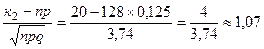 ,
,
 то
то 
Значение функции  также находим в специальной таблице (см. например
также находим в специальной таблице (см. например  , стр. 389). В таблице
, стр. 389). В таблице  Для отрицательных значений х используют эту же таблицу, учитывая, что
Для отрицательных значений х используют эту же таблицу, учитывая, что  является нечетной функцией, то есть
является нечетной функцией, то есть  Итак,
Итак, 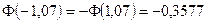 . Отсюда
. Отсюда 
Ответ: 
Правила выбора варианта контрольной работы, ее оформление и зачета
1. В процессе изучения высшей математики студент первого курса должен выполнить две контрольные работы, задачи второй из которых содержатся в разделе «Варианты контрольной работы». Не следует приступать к выполнению контрольного задания до решения достаточного количества задач по учебному материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.
2. Контрольные работы должны быть оформлены в соответствии с настоящими правилами. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.
3. Каждую контрольную работу следует выполнять в отдельной тетради, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
4. На обложке тетради должны быть разборчиво написаны фамилия, имя, и отчество студента, факультет (институт), номер группы, название дисциплины (высшая математика), номер контрольной работы, номер варианта и домашний адрес студента. В конце работы следует поставить дату ее выполнения и расписаться.
5. Номер варианта контрольной работы, которую выполняет студент, должен совпадать с последней цифрой номера его зачетной книжки.
6. Решения задач надо располагать в порядке возрастания номеров. Условия задач следует переписать в тетрадь.
7. При решении задач нужно обосновать каждый этап решения исходя из теоретических положений курса.
Решение задач и примеров следует излагать подробно, объясняя все выполненные действия и используемые формулы. Решение каждой задачи должно доводиться до окончательного ответа, которого требует условие. В промежуточные вычисления не следует вводить приближенные значения корней, числа p, e и т. д.
Полученный ответ следует проверить способами, вытекающими из существа данной задачи. Так, например, вычислив неопределенный интеграл, нужно проверить, равна ли подынтегральная функция производной от полученной первообразной. Полезно также, если это возможно, решить задачу несколькими способами и сравнить полученные результаты.
8. Срок проверки контрольных работ – 10 рабочих дней. Студенты обязаны сдавать письменные контрольные работы не позднее, чем за 10 дней до начала экзаменационной сессии. В противном случае они не будут допущены к зачетам и экзаменам.
9. После получения прорецензированной работы студент должен исправить все отмеченные рецензентом ошибки и недочеты, внести в решения задач рекомендуемые рецензентом изменения или дополнения и прислать работу для повторной проверки. В связи с этим рекомендуем при выполнении контрольной работы оставить в конце тетради несколько чистых листов для внесения исправлений и дополнений впоследствии.
В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
При представленных на повторную проверку исправлениях обязательно должны находиться прорецензированная работа и рецензия на нее. Вносить исправления в сам текст работы после ее рецензирования запрещается.
10. Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять.
На экзамен студент должен явиться с рецензией на выполненную контрольную работу. Без предъявления преподавателю прорецензированных контрольных работ студент к экзамену не допускается.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНАМ.
Семестр.
1. Понятие функции.
2. Область определения и множество значений функции.
3. Обратная функция.
4. Сложная функция.
5. Возрастание и убывание функции.
6. Наибольшее и наименьшее значения функции.
7. Ограниченность функции.
8. Периодичность.
9. Четность и нечетность функции.
10. Различные способы задания функций.
11. Предел функции.
12. Предел суммы и разности функций.
13. Предел произведения функций.
14. Предел обратной функции.
15. Предел частного функций.
16. Односторонние пределы.
17. Замечательные пределы.
18. Непрерывность функции.
19. Точки разрыва.
20. Свойства непрерывных функций.
21. Определение производной.
22. Дифференцируемость и непрерывность функций.
23. Геометрический и физический смысл производной функции.
24. Свойства производной.
25. Правила дифференцирования суммы и разности.
26. Правило дифференцирования произведения функций.
27. Правило дифференцирования произведения частного функций.
28. Производная сложной функции
29. Правило дифференцирования обратной функции.
30. Формулы дифференцирования основных элементарных функций.
31. Дифференциал функции, его геометрический смысл.
32. Исследование функции с помощью дифференциального исчисления и построение графиков функций.
33. Горизонтальная асимптота графика функции.
34. Вертикальная асимптота графика функции.
35. Наклонная асимптота графика функции.
36. Условия возрастания и убывания функции.
37. Экстремумы функции (минимум и максимум).
38. Необходимые и достаточные условия существования экстремума.
39. Выпуклость графика функции вверх и вниз.
40. Наибольшие и наименьшие значения функции на отрезке.
41. Первообразная.
42. Неопределенный интеграл.
43. Интеграл суммы и разности двух функций.
44. Интеграл произведения функции и числа.
45. Таблица интегралов.
46. Замена переменной в неопределенном интеграле.
47. Вычисление интегралов от рациональных функций.
48. Формула интегрирования по частям.
49. Определенный интеграл,
50. Геометрический смысл, определенного интеграла
51. Свойства пределов интегрирования.
52. Формула Ньютона-Лейбница.
53. Формула замены переменной в определенном интеграле.
54. Интегрирование по частям для определенного интеграла.
55. Применение определенного интеграла к вычислению площадей плоских фигур.
56. Применение определенного интеграла к вычислению объёмов тел вращения.
57. Дифференциальные уравнения.
58. Общий вид решения дифференциального уравнения с разделяющимися переменными.
59. Пространство решений линейного однородного дифференциального уравнения.
60. Общий вид решения линейного дифференциального уравнения.
Семестр.
1. N-мерное арифметическое пространство Rn.
2. Геометрический смысл пространств R2 и R3.
3. Векторы.
4. Длина вектора.
5. Линейные операции над векторами.
6. Скалярное произведение векторов.
7. Линейно зависимые и линейно не зависимые системы векторов.
8. Геометрический смысл линейной зависимости векторов.
9. Базис и ранг системы векторов.
10. Ортогональный и ортонормированный базисы.
11. Представление вектора в координатной форме.
12. Действия с векторами, заданными в координатной форме.
13. Угол между векторами.
14. Разложение вектора по произвольному базису.
15. Общее уравнение прямой.
16. Уравнение прямой с угловым коэффициентом.
17. Угол между прямыми, условия параллельности и перпендикулярности прямых.
18. Расстояние от точки до прямой.
19. Понятие о кривых второго порядка: окружность, эллипс, гипербола, парабола.
20. Прямая и плоскость в пространстве R3.
21. Расстояние от точки до плоскости.
22. Векторное, параметрическое, каноническое уравнения прямой в R3.
23. Матрицы, определение.
24. Умножение матрицы на число.
25. Сумма и разность матриц.
26. Произведение матриц.
27. Транспонирование.
28. Обратная матрица.
29. Определитель матрицы 2 на 2.
30. Определитель матрицы 3 на 3.
31. Определитель n-го порядка.
32. Миноры, алгебраические дополнения.
33. Способы вычисления обратной матрицы
34. Ранг матрицы.
35. Линейные уравнения с n неизвестными.
36. Условия совместности и определенности СЛУ.
37. Матричная запись системы линейных уравнений.
38. Решение системы линейных уравнений с помощью обратной матрицы.
39. Формулы Крамера.
40. Метод Гаусса.
41. Метод обратной матрицы.
42. Однородные системы линейных уравнений.
43. Пространство решений системы однородных линейных уравнений.
44. Общее решение неоднородной системы линейных уравнений.
45. Теорема Кронекера – Капелли.
46. Допустимое, базисное, опорное решение системы линейных уравнений.
47. Системы линейных неравенств с n неизвестными, их геометрический смысл.
48. Геометрический метод решения системы линейных неравенств с двумя переменными.
49. Выпуклые множества.
50. Основная задача линейного программирования.
51. Сумма множеств.
52. Разность множеств.
53. Симметрическая разность множеств.
54. Дополнение к множеству.
55. Произведение множеств.
56. Проверка тождеств в алгебре множеств.
57. Характеристическая функция множества.
58. Проверка тождеств с помощью характеристических функций.
59. Проверка множеств с помощью таблиц истинности.
60. Геометрическая интерпретация операций с множествами.
Семестр.
1. Понятие случайного события.
2. Виды событий.
3. Элементарные исходы.
4. Классическое определение вероятности.
5. Свойства вероятности.
6. Перестановки.
7. Сочетания.
8. Размещения.
9. Правило суммы.
10. Правило произведения.
11. Колмогоровское определение вероятности.
12. Сумма событий.
13. Произведение событий.
14. Противоположное событие.
15. Несовместные события.
16. Независимые события.
17. Попарно независимые события.
18. Теорема сложения для несовместных событий.
19. Теорема умножения.
20. Теорема умножения для независимых событий.
21. Теорема сложения для совместных событий.
22. Полная группа событий.
23. Вероятность появления одного из нескольких независимых событий.
24. Сумма вероятностей противоположных событий.
25. Формула полной вероятности.
26. Формула Байеса.
27. Формула Бернулли.
28. Локальная теорема Лапласа.
29. Интегральная теорема Лапласа.
30. Понятие случайной величины.
31. Дискретные случайные величины.
32. Закон распределения дискретной случайной величины.
33. Функция распределения, ее свойства, график.
34. Биноминальное распределение.
35. Распределение Пуассона.
36. Непрерывные случайные величины.
37. Плотность распределения случайной величины.
38. Равномерное распределение,
39. Экспоненциальное распределение.
40. Независимость случайных величин.
41. Представление числа случайной величиной.
42. Сумма случайных величин.
43. Произведение случайных величин.
44. Разность случайных величин.
45. Математическое ожидание случайной величины.
46. Математическое ожидание числа.
47. Математическое ожидание суммы.
48. Математическое ожидание произведения.
49. Дисперсия случайной величины.
50. Дисперсия суммы.
51. Дисперсия разности.
52. Дисперсия произведения.
53. Статистическая совокупность. Выборки.
54. Статистическая функция распределения.
55. Оценка параметров.
56. Медиана.
57. Мода.
58. Понятие о доверительных интервалах.
59. Математические методы проверки гипотез.
60. Корреляция. Коэффициент корелляции.
61. Линейная регрессия.
62. Однофакторный анализ. Проверка зависимости факторов.
Не нашли, что искали? Воспользуйтесь поиском: