Решение систем линейных уравнений методом обратной матрицы

Метод обратной матрицы – это метод решения квадратных систем линейных уравнений, в которых определитель системы не равен нулю.

Рассмотрим систему:

Обозначим через матрицу коэффициентов при неизвестных, через и – матрицы-столбцы переменных и правой части.

; ; ; .

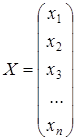Систему уравнений можно представить в матричной форме, она примет такой вид:

.

Умножим это равенство на обратную матрицу

, ,

Мы получили матричную запись решения системы линейных уравнений, из которой можно заключить следующее: чтобы квадратную систему линейных уравнений решить методом обратной матрицы, необходимо найти обратную матрицу и умножить ее “слева” на матрицу-столбец .

Пример 9. Решить систему методом обратной матрицы

.

Ранее мы нашли обратную для матрицы – в примере 8.

, , .

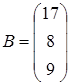
Проверка показывает, что система решена верно.

Не нашли, что искали? Воспользуйтесь поиском: