Системы линейных неоднородных уравнений

Пусть дана произвольная система линейных уравнений:

Обозначим через матрицу, составленную из коэффициентов при неизвестных системы, а через 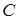– матрицу, полученную из присоединением столбца свободных членов:

Матрица называется матрицей системы уравнений, а матрица 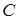– расширенной матрицей этой системы.

Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее матрицы равнялся рангу расширенной матрицы 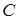. Если ранг матрицы равен рангу матрицы 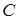и равен числу неизвестных, то система имеет единственное решение. Если ранг матрицы равен рангу матрицы 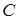, но меньше числа неизвестных, то система имеет бесконечное множество различных решений.

Замечание. При исследовании на совместность системы линейных уравнений иногда удобнее начинать с вычисления ранга расширенной матрицы 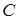, тогда попутно легко установить и ранг матрицы .

Пример 14. Установить совместность системы уравнений и число решений:

Составим расширенную матрицу и, пользуясь правилом прямоугольника, найдем ранг

Ранг матрицы системы равен рангу расширенной матрицы – значит, система линейных уравнений совместна. Поскольку ранг равен числу переменных, то система имеет единственное решение – оно было найдено раньше с помощью метода Гаусса.

Пример 15. Проверить, совместна ли система уравнений и каким будет решение.

.

Система уравнений совместна, а т.к. ранг меньше числа переменных, то она имеет бесчисленное множество решений. Оставим первые два линейно независимых уравнения и перенесем слагаемое с в правую часть ( называется свободной переменной).

Решаем по правилу Крамера

;

.

Задавая любые значения , будем получать множество значений и . Например, пусть , тогда . Или пусть , .

Не нашли, что искали? Воспользуйтесь поиском: