Системы линейных однородных уравнений

Система линейных уравнений называется однородной, если свободные члены уравнений равны нулю. Такая система имеет вид

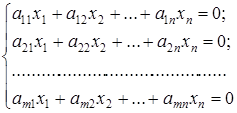
Однородная система всегда совместна. Это следует из теоремы Кронекера-Капелли. Кроме того, значения неизвестных 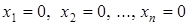образуют решение системы, оно называется нулевым или тривиальным.

Для однородной системы важно установить, имеет ли она ненулевые решения. Ответ на этот вопрос следует из второй теоремы Кронекера-Капелли.

Следствие 1. Если в однородной системе число неизвестных больше числа уравнений, то система, помимо нулевого решения, обладает еще и ненулевыми.

Следствие 2. Для того чтобы однородная система 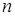линейных уравнений с 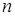неизвестными обладала и ненулевыми решениями, необходимо и достаточно, чтобы определитель системы равнялся нулю.

Пример 16. Решить однородную систему четырех линейных уравнений с четырьмя неизвестными

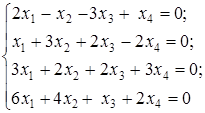
Найдем ранг матрицы системы

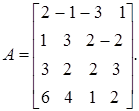
Если сложить первые три строки и эту сумму вычесть из четвертой строки, получим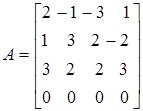

Как, видим определитель матрицы будет равен нулю, и ранг будет меньше .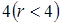

Так как есть определитель третьего порядка, отличный от нуля,

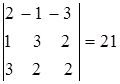
то ранг матрицы равен трем. Следовательно, система имеет и ненулевые решения.

Заданная система эквивалентна такой:

Мы взяли первые три линейно независимых уравнения с определителем, не равным 0. Так как определитель, состоящий из коэффициентов при неизвестных 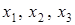, отличен от нуля, то, перенеся 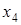в правую часть, решим систему трех уравнений с тремя неизвестными

Решим систему по правилу Крамера:

,

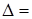
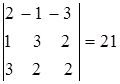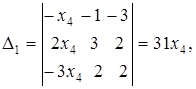
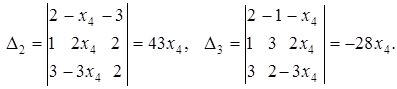
Следовательно,

.

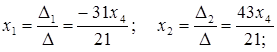
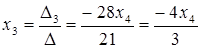Для контроля можно подставить это решение во все четыре заданные уравнения системы и убедиться, что система решена правильно. Для нахождения любого конкретного решения необходимо задать значение 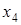и подсчитать соответствующие значения других переменных.

Не нашли, что искали? Воспользуйтесь поиском: