
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Векторные величины и действия над ними
Величины, для характеристики которых достаточно задать их численное значение (например, температура, объем, масса тела, плотность и т.д.), называются скалярными величинами или скалярами.
Величины, которые кроме своей абсолютной величины характеризуются еще и направлением (например, сила, скорость, ускорение и т.д.), называют векторными. Выбрав единицу длины, векторные величины можно изображать геометрическими векторами.
Вектором называется направленный отрезок или упорядоченная пара точек. На чертеже вектор изображается отрезком прямой, на котором отмечено направление (рис.1). Над буквенным обозначением вектора, имеющего началом точку  , а концом точку
, а концом точку  , ставится стрелка:
, ставится стрелка:  . Вектор обозначают также и одной буквой, но напечатанной жирным шрифтом:
. Вектор обозначают также и одной буквой, но напечатанной жирным шрифтом:  или
или  .
.

| 
| 
| ||||||||||||||||||||||||

| ||||||||||||||||||||||||||

| ||||||||||||||||||||||||||

| а | |||||||||||||||||||||||||

| ||||||||||||||||||||||||||
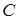
| ||||||||||||||||||||||||||
| Рис. 1 | Рис. 2 |
К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают. Он обозначается  .
.
Расстояние между началом и концом вектора называется его длиной или модулем. Модуль вектора обозначается так:  или
или  .
.
Векторы, параллельные одной прямой или лежащие на прямой, называются коллинеарными, а векторы, расположенные в одной плоскости или параллельные одной и той же плоскости, – компланарными. Радиус-вектором точки  называется вектор, направленный из начала координат в точку
называется вектор, направленный из начала координат в точку  (это вектор
(это вектор  ).
).
Два вектора 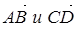 (рис. 2) называются равными, если они коллинеарны, одинаково направлены и равны по длине. Равенство векторов записывается так:
(рис. 2) называются равными, если они коллинеарны, одинаково направлены и равны по длине. Равенство векторов записывается так:  . Если векторы имеют одинаковую длину, но противоположные направления, то они называются взаимнопротивоположными.
. Если векторы имеют одинаковую длину, но противоположные направления, то они называются взаимнопротивоположными.
Из определения равенства векторов следует, что при параллельном переносе вектора получается вектор, равный исходному. Поэтому начало вектора можно помещать в любую точку пространства. Векторы, начало которых при параллельном переносе можно помещать в любую точку пространства, называют свободными.
Над векторами можно выполнить различные линейные действия:
а) Произведением вектора а на число  называется вектор
называется вектор  , имеющий (при
, имеющий (при  ) направление вектора
) направление вектора 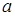 , если
, если  , и противоположное направление, если
, и противоположное направление, если  . Длина вектора
. Длина вектора  равна произведению длины вектора а на модуль числа
равна произведению длины вектора а на модуль числа  . Следовательно, вектор
. Следовательно, вектор  коллинеарен вектору
коллинеарен вектору 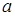 . Результат умножения вектора
. Результат умножения вектора 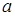 на число
на число  записывается равенством
записывается равенством  .
.
Отметим, что вектор, длина которого равна единице, называется единичным или ортом. Для любого вектора 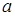 имеет место равенство
имеет место равенство  , где
, где  – единичный вектор, указывающий направление.
– единичный вектор, указывающий направление.
б) Суммой векторов 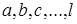 называется новый вектор
называется новый вектор  , который замыкает ломаную линию, построенную из данных векторов так, что начало каждого из последующих векторов суммы совмещается с концом предыдущего. Замыкающий вектор
, который замыкает ломаную линию, построенную из данных векторов так, что начало каждого из последующих векторов суммы совмещается с концом предыдущего. Замыкающий вектор  направлен из начала первого вектора суммы к концу последнего (рис. 3).
направлен из начала первого вектора суммы к концу последнего (рис. 3).

| 
| 
| |||||||||||||||||||||||
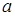
| 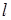
| ||||||||||||||||||||||||

| |||||||||||||||||||||||||
| Рис. 3 |
Для суммы векторов принята запись  .
.
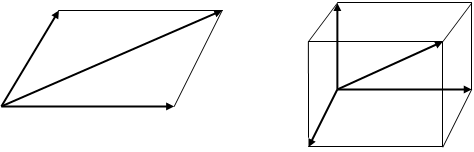
Правило параллелограмма для сложения двух векторов: сумма двух векторов  и
и 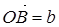 , приведенных к общему началу О (рис. 4), есть вектор-диагональ
, приведенных к общему началу О (рис. 4), есть вектор-диагональ  параллелограмма, построенного на данных векторах.
параллелограмма, построенного на данных векторах.

| 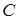
| 
| |||||||||||||||||||||||||
|

| 
| |||||||||||||||||||||||||
| 
| ||||||||||||||||||||||||||
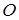
| 
| ||||||||||||||||||||||||||
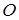
| 
| ||||||||||||||||||||||||||

| 
| ||||||||||||||||||||||||||

| |||||||||||||||||||||||||||
| Рис. 4 | Рис. 5 | ||||||||||||||||||||||||||
Правило параллелепипеда для сложения трех векторов: сумма трех некомпланарных векторов  ,
, 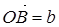 ,
,  , приведенных к общему началу О (рис. 5), есть вектор-диагональ
, приведенных к общему началу О (рис. 5), есть вектор-диагональ  параллелепипеда, построенного на данных векторах:
параллелепипеда, построенного на данных векторах:

в) Разностью двух векторов 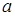 и
и  называется такой вектор
называется такой вектор  , который при сложении с вектором
, который при сложении с вектором  дает вектор
дает вектор 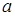 , т.е.
, т.е. 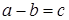 , если
, если  . Вектор разности будет являться второй диагональю параллелограмма, направленной из конца вычитаемого к концу уменьшаемого.
. Вектор разности будет являться второй диагональю параллелограмма, направленной из конца вычитаемого к концу уменьшаемого.
Чтобы построить разность  , приведем векторы
, приведем векторы  и
и 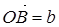 к общему началу О (рис. 6), тогда разность представляет собой вектор, соединяющий их концы и направленный от “вычитаемого” к “уменьшаемому”.
к общему началу О (рис. 6), тогда разность представляет собой вектор, соединяющий их концы и направленный от “вычитаемого” к “уменьшаемому”.
Заметим, что линейные операции над векторами установлены в соответствии с физическими законами, приводящими к сложению векторных величин или умножению их на число.

| ||||||||||||||||||||||||||

| ||||||||||||||||||||||||||

| 
| 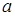
| 
|

| ||||||||||||||||||||||

| 
| |||||||||||||||||||||||||
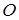
| 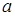
| 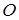  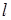 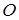  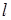
| ||||||||||||||||||||||||
| Рис. 6 | Рис. 7 |
г) Проекцией вектора  на ось
на ось  называется длина отрезка, заключенного между проекциями начала и конца вектора на эту ось (рис. 7).
называется длина отрезка, заключенного между проекциями начала и конца вектора на эту ось (рис. 7).
Проекция вектора 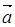 на ось
на ось  равна произведению модуля проектируемого вектора на косинус угла между положительным направлением оси и вектором.
равна произведению модуля проектируемого вектора на косинус угла между положительным направлением оси и вектором.
Обозначают проекции так: 

 .
.
Выразим проекции вектора 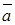 на оси координат
на оси координат
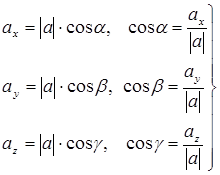 направляющие косинусы вектора
направляющие косинусы вектора
где  – это углы вектора с осями координат.
– это углы вектора с осями координат.
д) Скалярным произведением двух векторов  называется число, равное произведению их модулей на косинус угла между векторами
называется число, равное произведению их модулей на косинус угла между векторами 

Из формул для проекций получаем другое выражение скалярного произведения
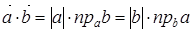
Скалярное произведение двух векторов равно произведению модуля одного из них на проекцию второго на направление первого вектора.
Скалярное произведение векторов обладает такими свойствами:
1.  – скалярное произведение коммутативно.
– скалярное произведение коммутативно.
2. Для любого вектора  скалярный квадрат равен квадрату модуля:
скалярный квадрат равен квадрату модуля:  .
.
3.  – скалярное произведение дистрибутивно относительно сложения.
– скалярное произведение дистрибутивно относительно сложения.
4. 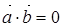 – скалярное произведение равно нулю тогда и только тогда, когда векторы перпендикулярны или хотя бы один из них равен нулю.
– скалярное произведение равно нулю тогда и только тогда, когда векторы перпендикулярны или хотя бы один из них равен нулю.
5.  – скалярный множитель можно выносить за знак скалярного произведения.
– скалярный множитель можно выносить за знак скалярного произведения.
е) Разложение вектора по базису – это представление одного вектора через другие, называемые базисными.
Под базисом на плоскости подразумевается два неколлинеарных вектора плоскости, взятых в определенном порядке. Под базисом в пространстве понимается три некомпланарных вектора, взятых в определенном порядке. Если на плоскости выбраны два базисных вектора  и
и  , то любой вектор плоскости может быть представлен в виде:
, то любой вектор плоскости может быть представлен в виде:
 .
.
Аналогично в пространстве: если базисными будут векторы  , то любой вектор пространства выражается так:
, то любой вектор пространства выражается так:  . Если на плоскости или в пространстве выбрана прямоугольная декартовая система координат, в которой базисные векторы попарно перпендикулярны, то любой вектор можно записать так:
. Если на плоскости или в пространстве выбрана прямоугольная декартовая система координат, в которой базисные векторы попарно перпендикулярны, то любой вектор можно записать так:  или
или  , где
, где  – единичные векторы соответствующих осей координат.
– единичные векторы соответствующих осей координат.
Пример 17. По сторонам ОА и ОВ прямоугольника ОАСВ отложены единичные векторы 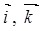 . Выразить через них векторы
. Выразить через них векторы  если длина
если длина  .
.
| Решение: Рассмотрим рис. 8 и найдем векторы: | |
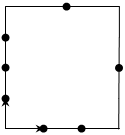  
  
  
|   


   Рис. 8
Рис. 8
|
Пример 18. В равнобедренной трапеции ОАСВ угол 
 ; M и N – середины сторон ВС и АС. Выразить векторы
; M и N – середины сторон ВС и АС. Выразить векторы  и
и  через
через  и
и  - единичные векторы
- единичные векторы  (рис. 9).
(рис. 9).

| 
| 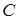
| |||||||||||||||||

| |||||||||||||||||||

| 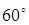
| ||||||||||||||||||
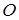
| 
| 
| 
| 
| |||||||||||||||
| Рис. 9 |
Решение.
 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
 .
.
Пример 19. Три вектора  расположены в одной плоскости.
расположены в одной плоскости.  Известно, что векторы
Известно, что векторы  и
и  составляют с вектором
составляют с вектором  углы в 600. Определить угол между векторами
углы в 600. Определить угол между векторами  и
и  и длину вектора
и длину вектора  .
.
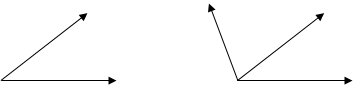 Решение. Векторы
Решение. Векторы  и
и  могут находиться по одну сторону от
могут находиться по одну сторону от  , (тогда угол между ними равен
, (тогда угол между ними равен 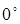 ) и по разные стороны (тогда между ними угол в
) и по разные стороны (тогда между ними угол в  ):
):

| 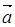
| ||||||||||||||||||||||||||

| |||||||||||||||||||||||||||
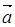
| 
| ||||||||||||||||||||||||||
| Рис.10 | Рис. 11 | ||||||||||||||||||||||||||
Соответственно длина вектора для каждого случая будет своя:
а) 

 ,
, 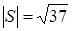 .
.
б) 
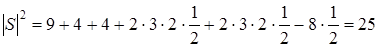 ,
,  .
.
4.2. Векторы в координатной форме
Координатами вектора называются проекции его на координатные оси. Если обозначить проекции вектора  через
через  то вектор через его координаты записывают так
то вектор через его координаты записывают так
 или
или 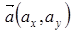 .
.
Всякий вектор можно представить в виде его разложения по координатным осям:  , где
, где  - единичные векторы осей,
- единичные векторы осей,  - координаты вектора.
- координаты вектора.
Если для вектора  известны координаты его начала
известны координаты его начала  и координаты его конца
и координаты его конца  , то координаты вектора равны разностям соответствующих координат конца и начала вектора, т.е.
, то координаты вектора равны разностям соответствующих координат конца и начала вектора, т.е. 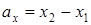 ,
,  ,
,  .
.
Над векторами, представленными в координатной форме, можно выполнять различные линейные действия.
а) Если вектор  , имеющий координаты
, имеющий координаты  умножить на число
умножить на число  , то на это число следует умножить каждую координату вектора
, то на это число следует умножить каждую координату вектора
 .
.
б) Координаты алгебраической суммы векторов равны алгебраической сумме соответствующих координат составляющих векторов. Если векторы 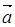 и
и  заданы своими координатами
заданы своими координатами  , то их сумму и разность определяют так:
, то их сумму и разность определяют так:  .
.
в) Модуль вектора, заданного своими координатами, равен корню квадратному из суммы квадратов его проекций. Пусть задан вектор  , т.е.
, т.е.  . Используем свойство скалярного произведения:
. Используем свойство скалярного произведения:  . Подставим значение векторов и перемножим
. Подставим значение векторов и перемножим 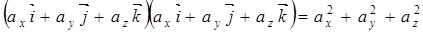 . В результате получим
. В результате получим  .
.
Если вектор задан координатами начала и конца, то
 .
.
Эта формула выражает длину вектора или расстояние между двумя точками.
г) Рассмотрим деление отрезка в данном отношении (рис. 12). Пусть даны точки  и
и  . Точка
. Точка  делит отрезок
делит отрезок  в отношении
в отношении  , т.е.
, т.е.  .
.

| z | Найдем координаты векторов  и и  : :
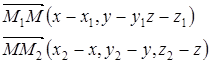
| |||||||||||
| M1 | M M2 | ||||||||||||
| х | |||||||||||||
| y | Рис. 12 |
Запишем равенство  через координаты:
через координаты:

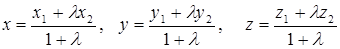
| – формулы для определения координат точки 
|
Если  , получаем частный случай формул:
, получаем частный случай формул:
 . .
|
д) Рассмотрим скалярное произведение векторов в координатной форме.
Пусть  и
и  , т.е.
, т.е.  ,
, 
 .
.
Скалярное произведение векторов равно сумме произведений их одноименных координат.
е) Найдем углы вектора с координатными осями (направляющие косинусы).
 ,
,  ,
,
 ,
,

| – свойство направляющих косинусов |
ж) Определим углы между векторами. Исходя из скалярного произведения и его выражения в координатной форме, получим соответствующую формулу.
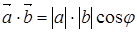 ,
,
 ,
,
 .
.
Векторы будут перпендикулярны, если  , т.е. сумма произведений их одноименных координат равна нулю.
, т.е. сумма произведений их одноименных координат равна нулю.
Чтобы вектор  был параллелен вектору
был параллелен вектору 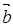 , необходимо и достаточно выполнения равенства:
, необходимо и достаточно выполнения равенства:  или
или  , или
, или  . Для параллельности векторов необходимо и достаточно, чтобы их координаты были пропорциональны. Если знаменатель равен 0, то это соотношение не рассматривается.
. Для параллельности векторов необходимо и достаточно, чтобы их координаты были пропорциональны. Если знаменатель равен 0, то это соотношение не рассматривается.
Пример 20. Даны векторы  ,
,  . Найти
. Найти  ,
,  ,
,  .
.
Решение.
 ,
,
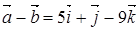 .
.
Ответ:  ;
;  ;
;  ;
;  .
.
Пример 21. Заданы две точки:  ,
,  . Найти проекции вектора
. Найти проекции вектора  на оси и его направляющие косинусы?
на оси и его направляющие косинусы?
Решение.
 ,
, 
 .
.
Пример 22. Заданы два вектора  ,
,  . Найти скалярное произведение и угол между векторами.
. Найти скалярное произведение и угол между векторами.
Решение.
 ,
,
 ,
,  ,
,
 .
.
Пример 23. Даны 4 точки: 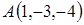 ,
,  ,
,  ,
,  . Найти угол между векторами
. Найти угол между векторами  и
и  .
.
Решение. Найдем векторы  и
и  .
.
 ,
,
 ,
,  ,
,
 .
.
Пример 24. Даны векторы: 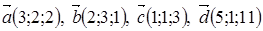 . Показать, что векторы
. Показать, что векторы  могут быть базисом и выразить вектор
могут быть базисом и выразить вектор  в этом базисе.
в этом базисе.
Решение.
а) Чтобы векторы  могли служить базисом, они должны быть линейно-независимыми, т.е. ранг матрицы, составленной из координат вектора, должен равняться 3. Найдем определитель матрицы.
могли служить базисом, они должны быть линейно-независимыми, т.е. ранг матрицы, составленной из координат вектора, должен равняться 3. Найдем определитель матрицы.
 .
.
Поскольку  , то ранг равен 3, и векторы могут служить базисом.
, то ранг равен 3, и векторы могут служить базисом.
б) Выразим вектор  в базисе:
в базисе:  . В координатной форме получим систему и решим ее:
. В координатной форме получим систему и решим ее:

 ;
;
 .
.
Получим выражение вектора  в базисе:
в базисе:  .
.
4.3. Прямая линия на плоскости
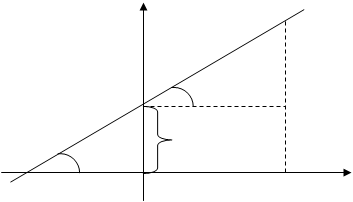
а) Уравнение прямой с угловым коэффициентом (рис. 13).
Тангенс угла наклона прямой к оси  называется угловым коэффициентом этой прямой.
называется угловым коэффициентом этой прямой.
| 
| 
| |||||||||||||||||||||||||

| |||||||||||||||||||||||||||

| 
| ||||||||||||||||||||||||||

| 
| ||||||||||||||||||||||||||

| |||||||||||||||||||||||||||

| 
|
Рис. 13
Пусть дана прямая, пересекающая ось  под углом
под углом  - текущая (произвольная) точка прямой, ее координаты
- текущая (произвольная) точка прямой, ее координаты 

 .
.
|

Не нашли, что искали? Воспользуйтесь поиском:
