ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Исследуем общее уравнение. 3 страница
| а) 3; | б) 1; | в) 2; | г) 4. |
8. Показать совместимость системы, найти ее решение методами Крамера, Гаусса, обратной матрицы
| а) (1; 1; 1); | б) (0; 0; 1); | в) другой ответ; | г) (2; 1; 0). |
Вариант 10
1. Пользуясь свойствами определителя, не проводя вычислений, указать, какой из определителей не равен нулю:
а)  ;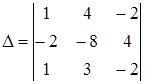
| б)  ;
|
в)  ;
| г)  .
|
2. Найти значение определителя методом Саррюса, с помощью теоремы разложения, дописыванием столбцов:
| а) 10; | б) 5; | в) 15; | г) другой ответ. |
3. С помощью теоремы разложения найти значение определителя:
| а) 63; | б) -31; | в) 176; | г) другой ответ. |
4. Найти 
, если 
и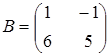 
.
а)  ;
| б)  ;
| в)  ;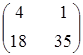
| г) другой ответ. |
5. Вычислить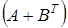 
, если 
и 
.
а)  ;
| б)  ;
| в)  ;
| г) другой ответ. |
6. Определите, какая из представленных матриц является обратной по отношению по отношению к данной матрице 
и сделайте проверку.
а)  ;
| б)  ;
|
в)  ;
| г) другой ответ. |
7. Определить ранг матрицы 
.
| а) 3; | б) 2; | в) 1; | г) 4. |
8. Показать совместимость системы, найти ее решение методами Крамера, Гаусса, обратной матрицы
| а) другой ответ; | б) (-1; 0; 1); | в) (0; 2; 1); | г) (1; 2; -1). |
Вариант 11
1. Пользуясь свойствами определителя, не проводя вычислений, указать, какие из определителей равны нулю:
а)  ;
| б)  ;
|
в)  ;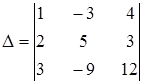
| г)  .
|
2. Найти значение определителя методом Саррюса, с помощью теоремы разложения, дописыванием столбцов:
| а) 20; | б) 40; | в) -10; | г) другой ответ. |
3. С помощью теоремы разложения найти значение определителя:
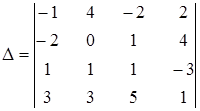
| а) 93; | б) 46; | в) другой ответ; | г) 186. |
4. Найти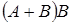 
, если 
и 
.
а)  ;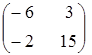
| б)  ;
| в)  ;
| г) другой ответ. |
5. Вычислить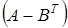 
, есл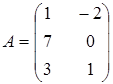и 
и 
.
а)  ;
| б)  ;
| в)  ;
| г) другой ответ. |
6. Определите, какая из представленных матриц является обратной по отношению по отношению к данной матрице и сделайте проверку.
а)  ;
| б)  ;
|
в)  ;
| г) другой ответ. |
7. Определить ранг матрицы 
.
| а) 1; | б) 2; | в) 3; | г) 4. |
8. Показать совместимость системы, найти ее решение методами Крамера, Гаусса, обратной матрицы
| а) (1; 2; 2); | б) (2; 1; 2); | в) другой ответ; | г) (2; 2; 1). |
Вариант 12
1. Пользуясь свойствами определителя, не проводя вычислений, указать, какие из определителей равны нулю:
а)  ;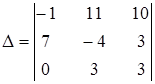
| б)  ;
|
в)  ;
| г)  .
|
2. Найти значение определителя методом Саррюса, с помощью теоремы разложения, дописыванием столбцов:
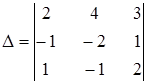
| а) 15; | б) 30; | в) -5; | г) другой ответ. |
3. С помощью теоремы разложения найти значение определителя:
| а) 133; | б) -266; | в) 17; | г) другой ответ. |
4. Найти 
, если 
и 
.
а)  ;
| б)  ;
| в)  ;
| г) другой ответ. |
5. Вычислить 
, если 
и 
.
а)  ;
| б)  ;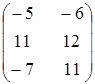
| в)  ;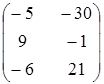
| г) другой ответ. |
6. Определите, какая из представленных матриц является обратной по отношению по отношению к данной матрице и сделайте проверку.
а)  ;
| б)  ;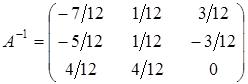
|
в)  ;
| г) другой ответ. |
7. Определить ранг матрицы 
.
| а) 3; | б) 4; | в) 1; | г) 2. |
8. Показать совместимость системы, найти ее решение методами Крамера, Гаусса, обратной матрицы
| а) (1; -2; 0); | б) (0; 0; 0); | в) (1; 1; 1); | г) другой ответ. |
Вариант 13
1. Пользуясь свойствами определителя, не проводя вычислений, указать, какие из определителей равны нулю:
а)  ;
| б)  ;
|
в)  ;
| г)  .
|
2. Найти значение определителя методом Саррюса, с помощью теоремы разложения, дописыванием столбцов:
| а) 13; | б) -26; | в) 17; | г) другой ответ. |
3. С помощью теоремы разложения найти значение определителя:
| а) 93; | б) 100; | в) -13; | г) другой ответ. |
4. Найти 
, если 
и 
.
а)  ;
| б)  ;
| в)  ;
| г) другой ответ. |
5. Вычислить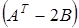 
, если 
и 
.
а)  ;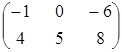
| б)  ;
| в)  ;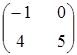
| г) другой ответ. |
6. Определите, какая из представленных матриц является обратной по отношению по отношению к данной матрице и сделайте проверку.
а)  ;
| б)  ;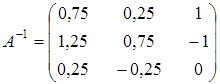
|
в)  ;
| г) другой ответ. |
7. Определить ранг матрицы 
.
| а) 4; | б) 3; | в) 1; | г) 2. |
8. Показать совместимость системы, найти ее решение методами Крамера, Гаусса, обратной матрицы
| а) (0; 1; 0); | б) (-1; 1; 1); | в) другой ответ; | г) (1; -1; -1). |
Вариант 14
1. Пользуясь свойствами определителя, не проводя вычислений, указать, какие из определителей равны нулю:
а)  ;
| б)  ;
|
в)  ;
| г)  .
|
2. Найти значение определителя методом Саррюса, с помощью теоремы разложения, дописыванием столбцов:
| а) 3; | б) - 4; | в) 2; | г) другой ответ. |
3. С помощью теоремы разложения найти значение определителя:
| а) -30; | б) 21; | в) - 16; | г) другой ответ. |
4. Найти 
, если 
и 
.
а)  ;
| б)  ;
| в)  ;
| г) другой ответ. |
5. Вычислить 
, если 
и 
.
а)  ;
| б)  ;
| в) другой ответ; | г)  .
|
6. Определите, какая из представленных матриц является обратной по отношению по отношению к данной матрице и сделайте проверку.
а)  ;
| б)  ;
|
в)  ;
| г) другой ответ. |
7. Определить ранг матрицы 
.
| а) 1; | б) 2; | в) 4; | г) 3. |
8. Показать совместимость системы, найти ее решение методами Крамера, Гаусса, обратной матрицы
| а) (1; 4; 4); | б) (0; 6; 0); | в) (-2; 1; 1); | г) другой ответ. |
Вариант 15
1. Пользуясь свойствами определителя, не проводя вычислений, указать, какие из определителей равны нулю:
а)  ;
| б)  ;
|
в)  ;
| г)  .
|
2. Найти значение определителя методом Саррюса, с помощью теоремы разложения, дописыванием столбцов:
| а) 14; | б) -17; | в) другой ответ; | г) 7. |
3. С помощью теоремы разложения найти значение определителя:
| а) 31; | б) 19; | в) -16; | г) другой ответ. |
4. Найти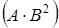 
, если 
и 
.
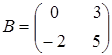а)  ;
| б)  ;
| в)  ;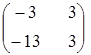
| г) другой ответ. |
5. Вычислить 
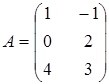, если 
и 
.
а)  ;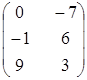
| б)  ;
| в)  ;
| г) другой ответ. |
6. Определите, какая из представленных матриц является обратной по отношению по отношению к данной матрице и сделайте проверку.
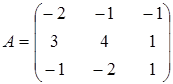
а)  ;
| б)  ;
|
в)  ;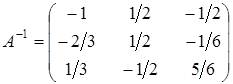
| г) другой ответ. |
7. Определить ранг матрицы 
.
| а) 1; | б) 3; | в) 2; | г) 4. |
8. Показать совместимость системы, найти ее решение методами Крамера, Гаусса, обратной матрицы
| а) (1; 3; 0); | б) (0; 5; 0); | в) другой ответ; | г) (1; 0; -1). |
Вариант 16
1. Пользуясь свойствами определителя, не проводя вычислений, указать, какие из определителей равны нулю:
а)  ;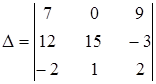
| б)  ;
|
в)  ;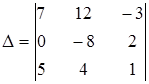
| г)  .
|
2. Найти значение определителя методом Саррюса, с помощью теоремы разложения, дописыванием столбцов:
| а) -6; | б) 8; | в) -10; | г) другой ответ. |
3. С помощью теоремы разложения найти значение определителя:
| а) 8; | б) 16; | в) -4; | г) другой ответ. |
4. Найти 
, если 
и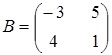 
.
а)  ;
| б)  ;
| в)  ;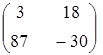
| г) другой ответ. |
5. Вычислить 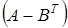, если 
и 
.
а)  ;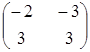
| б)  ;
| в)  ;
| г) другой ответ. |
6. Определите, какая из представленных матриц является обратной по отношению по отношению к данной матрице и сделайте проверку.
а)  ;
| б)  ;
|
в)  ;
| г) другой ответ. |
7. Определить ранг матрицы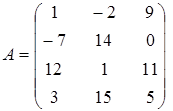 
.
| а) 1; | б) 3; | в) 4; | г) 2. |
8. Показать совместимость системы, найти ее решение методами Крамера, Гаусса, обратной матрицы
| а) (1; 1; 2); | б) другой ответ; | в) (0; 2; 1); | г) (1; 1; 0). |
Вариант 17
1. Пользуясь свойствами определителя, не проводя вычислений, указать, какие из определителей равны нулю:
а)  ;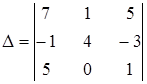
| б)  ;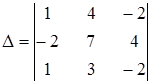
|
в)  ;
| г)  .
|
2. Найти значение определителя методом Саррюса, с помощью теоремы разложения, дописыванием столбцов:
| а) -3; | б) 17; | в) другой ответ; | г) 13. |
3. С помощью теоремы разложения найти значение определителя:
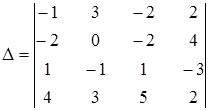
| а) -8; | б) 4; | в) -32; | г) другой ответ. |
4. Найти , если 
и .
а)  ;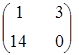
| б)  ;
| в)  ;
| г) другой ответ. |
5. Вычислить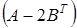 
, если 
и 
.
Не нашли, что искали? Воспользуйтесь поиском: