
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Исследуем общее уравнение. 1 страница
1) 
 – прямая проходит через начало координат;
– прямая проходит через начало координат;
2) 

 – прямая параллельна оси
– прямая параллельна оси 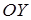 ;
;
а)  ,
,  ось
ось 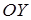
 – уравнение оси
– уравнение оси 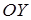 ;
;
3) 

 – прямая параллельна оси
– прямая параллельна оси  ;
;
а)  ,
, 
 - уравнение оси
- уравнение оси  .
.
д) Уравнение прямой в “отрезках” на осях.
Рассмотрим общее уравнение прямой в предположении, что ни один из коэффициентов  не равен 0.
не равен 0.
 .
.
Оно может быть приведено к специальному виду, удобному при решении задач. Перенесем 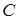 в другую часть уравнения
в другую часть уравнения
 .
.
Разделим на 
 или
или  .
.
|
Обозначим 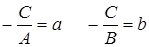 , тогда
, тогда
Получено уравнение “в отрезках” на осях: 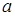 – величина отрезка, отсекаемого прямой на оси
– величина отрезка, отсекаемого прямой на оси  ,
,  – на оси
– на оси 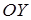 .
.
е) Нормальное уравнение прямой.
Этот вид уравнения получил свое название из-за нормали (перпендикуляра, проведенного из начала координат на прямую) (рис. 18).

| 
| ||||||||||||||||||||||||||

| |||||||||||||||||||||||||||

| 

| ||||||||||||||||||||||||||

| |||||||||||||||||||||||||||

| 
| ||||||||||||||||||||||||||

| 
| 
|
Рис. 18.
Обозначим  – расстояние от начала координат до прямой,
– расстояние от начала координат до прямой,  – угол нормали к оси
– угол нормали к оси  ,
,  - текущая точка –
- текущая точка – 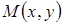 .
.
Из 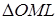 :
: 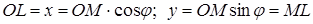 ,
,  – угол
– угол  с
с  .
.
Из 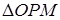 :
:  , преобразовав, получим:
, преобразовав, получим:
 ,
,
 .
.

| – нормальное уравнение. |
Главная особенность этого уравнения – сумма квадратов коэффициентов при неизвестных равна единице.
Замечание. Чтобы общее уравнение прямой преобразовать к нормальному виду, его необходимо умножить на нормирующий множитель.
 .
.
Знак берется противоположным свободному члену.
Например:
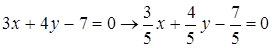 .
.
Следствие. Расстояние от точки до прямой
- если прямая задана нормальным уравнением:

и точка  , то расстояние точки А до прямой выразится так:
, то расстояние точки А до прямой выразится так:
 ;
;
- если прямая задана в общем виде, то
 .
.
Пример 25. В треугольнике заданы вершины:  ,
,  ,
,  . Найти длину и уравнение стороны
. Найти длину и уравнение стороны  ; длину и уравнение медианы
; длину и уравнение медианы  , точку пересечения медиан
, точку пересечения медиан  ; длину и уравнение высоты
; длину и уравнение высоты  .
.
Решение.
Схематично изобразим треугольник:

| 
| а) длину стороны  найдем по формуле найдем по формуле 

 . .
| ||||||||
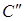
| ||||||||||

| ||||||||||

| ||||||||||
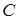
| ||||||||||

| ||||||||||
б) Уравнение стороны  составим, используя уравнение прямой, проходящей через две точки
составим, используя уравнение прямой, проходящей через две точки
 ,
,
 ,
,

| 
| – уравнение стороны 
|
в) Найдем точку  – середину
– середину  .
.
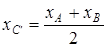 ,
,  ,
,  ,
,  .
.
г) Уравнение медианы  находим аналогично уравнению
находим аналогично уравнению  .
.


| – уравнение медианы  . .
|
д) Найдем точку  – она делит медиану
– она делит медиану  в отношении 2:1, т.е.
в отношении 2:1, т.е.  .
.

 .
.
е) Высота  перпендикулярна прямой
перпендикулярна прямой  – значит, их угловые коэффициенты удовлетворяют условию
– значит, их угловые коэффициенты удовлетворяют условию
 ,
,  .
.
Уравнение  составим на основе уравнения пучка прямых – ведь нам известна точка
составим на основе уравнения пучка прямых – ведь нам известна точка 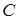 и угловой коэффициент
и угловой коэффициент  .
.
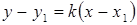
 ,
,

| – уравнение высоты  . .
|
ж) Длину высоты определим как расстояние от вершины 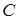 до прямой
до прямой  , представленной в общем виде:
, представленной в общем виде:

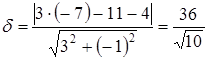 – длина высоты
– длина высоты  .
.
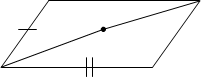
Пример 26. Даны две стороны параллелограмма  и точка пересечения диагоналей
и точка пересечения диагоналей  .
.
Найти уравнения двух других сторон.
Решение.

| 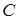
|
В условии даны уравнения смежных сторон (т.к. они не параллельны). Предположим, что это стороны  и и  . .
| |||||||
| 
| ||||||||

| 
| ||||||||
а) Определим вершину  как пересечение сторон
как пересечение сторон

 .
.
б) Найдем вершину 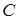 , зная, что
, зная, что  – середина
– середина 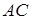


в) Уравнение  параллельно
параллельно  и проходит через точку
и проходит через точку 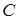
 .
.
Уравнения искомых сторон:
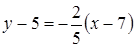 и
и 
 и
и 

| и | 
|
Задания для индивидуального решения
часть I. определители, Матрицы,
системы уравнений
В этом разделе предлагаются 30 вариантов заданий, позволяющих проверить практические навыки студентов по основным вопросам модуля: определители, матрицы, системы линейных уравнений и их совместимость. Каждому студенту предлагается 8 заданий с четырьмя вариантами ответов для самоконтроля усвоения материала. Задания можно рассматривать как своеобразные тесты для контроля знаний.
Вариант 1
1. Пользуясь свойствами определителя, не проводя вычислений, указать, какие из определителей равны нулю:
а) 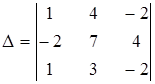 ; ;
| б)  ; ;
|
в)  ; ;
| г)  . .
|
2. Найти значение определителя методом Саррюса, с помощью теоремы разложения, дописыванием столбцов:

| а) 3; | б) –3; | в) 8; | г) другой ответ. |
3. С помощью теоремы разложения найти значение определителя:

| а) 16; | б) -5; | в) другой ответ; | г) 3. |
4. Найти  , если
, если  и
и  .
.
а)  ; ;
| б)  ; ;
| в)  ; ;
| г) другой ответ. |
5. Вычислить  , если
, если  и
и  .
.
а) 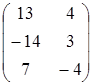 ; ;
| б)  ; ;
| в)  ; ;
| г) другой ответ. |
6. Определите, какая из представленных матриц является обратной по отношению по отношению к данной матрице  и сделайте проверку.
и сделайте проверку.

а)  ; ;
| б)  ; ;
|
в)  ; ;
| г) другой ответ. |
7. Определить ранг матрицы  .
.
| а) 4; | б) 2; | в) 3; | г) 1. |
8. Показать совместимость системы, найти ее решение методами Крамера, Гаусса, обратной матрицы
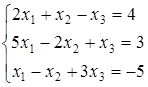
| а) (0; 6; 2); | б) (1;0;-2); | в) другой ответ; | г) (1; -1; 0). |
Вариант 2
1. Пользуясь свойствами определителя, не проводя вычислений, указать, какой из определителей не равен нулю:
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  . .
|
2. Найти значение определителя методом Саррюса, с помощью теоремы разложения, дописыванием столбцов:

| а) -1; | б) 3; | в) 1; | г) другой ответ. |
3. С помощью теоремы разложения найти значение определителя:
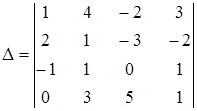
Не нашли, что искали? Воспользуйтесь поиском:
