
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретический блок.
Комбинаторика - ветвь математики, один из разделов теории вероятности, изучающая комбинации и перестановки предметов. Еще комбинаторику можно понимать как перебор возможных вариантов. Комбинаторика возникла в 17 веке. Долгое время она лежала вне основного русла развития математики.
С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов - во время работы.
Комбинаторные навыки оказались полезными и в часы досуга. Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие, в первую очередь, умения рассчитывать, составлять планы и опровергать планы противника.
Комбинаторика как наука стала развиваться в 18 веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов.
В современном обществе с развитием вычислительной техники комбинаторика “добилась” новых успехов. В настоящее время в образовательный стандарт по математике включены основы комбинаторики, решение комбинаторных задач методом перебора, составлением дерева вариантов (еще его называют “дерево возможностей”) с применением правила умножения. Так, например, “дерево возможностей” помогает решать разнообразные задачи, касающиеся перебора вариантов происходящих событий. Каждый путь по этому “дереву” соответствует одному из способов выбора, число способов выбора равно числу точек в нижнем ряду “дерева”. Правило умножения заключается в том, что для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В. В задачах по комбинаторике часто применяется такое понятие как факториал (в переводе с английского “factor” - “множитель”).
Итак, произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут:  !=
!=  .
.
В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.
Размещения.
Теорема 1. Общее количество различных наборов при выборе  элементов из
элементов из 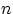 без возвращения и с учётом порядка равняется
без возвращения и с учётом порядка равняется

и называется числом размещений из 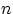 элементов по
элементов по  элементов.
элементов.
Перестановки.
Теорема 2. Если в множестве 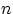 элементов, то существует ровно
элементов, то существует ровно  перестановок этих элементов.
перестановок этих элементов.
Сочетания.
Теорема 3. Общее количество различных наборов при выборе  элементов из
элементов из 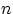 без возвращения и без учёта порядка равняется
без возвращения и без учёта порядка равняется

и называется числом сочетаний из 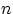 элементов по
элементов по  элементов.
элементов.
Все эти теоремы примем без доказательства (хотя их можно доказать!).
3. Блок практических заданий (выполнение заданий по алгоритму, типовые расчеты, ответы на контрольные вопросы, …).
Алгоритм решения:
ЗАДАЧИ:
1. В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе - мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье - чай и компот. Сколько различных обедов можно составить из указанных блюд?
1 способ. Перечислим возможные варианты:
| Чай(Ч) Компот (К) | Мясо с макаронами(М) | Рыба с картошкой(Р) | Курица с рисом(Кр) |
| Борщ (Б) | БМЧ/ БМК | БРЧ/БРК | БКрЧ/БКрК |
| Солянка(С) | СМЧ/ СМК | СРЧ/СРК | СКрЧ/СКрК |
| Грибной суп(Г) | ГМЧ/ГМК | ГРЧ/ГРК | ГКрЧ/ГКрК |
2 способ. Используя правило умножения, получаем: 3х3х2=18.
Ответ: 18 вариантов.
2. Свете на день рождения подарили 4 плюшевых игрушки, 2 мяча и 5 кукол. Мама положила все игрушки в большую коробку. Сколькими способами Света сможет достать из коробки 1 плюшевую игрушку, 1 мяч и 1 куклу?
1 способ. Обозначим мячи - М1, М2, игрушки - И1, И2, И3, И4, куклы - К1, К2, К3, К4, К5. Перечислим возможные варианты:
М1-И1-К1, М1-И1-К2, М1-И1-К3, М1-И1-К4, М1-И1-К5,
М1-И2-К1, М1-И2-К2, М1-И2-К3, М1-И2-К4, М1-И2-К5,
М1-И3-К1, М1-И3-К2, М1-И3-К3, М1-И3-К4, М1-И3-К5,
М1-И4-К1, М1-И4-К2, М1-И4-К3, М1-И4-К4, М1-И4-К5
М2-И1-К1, М2-И1-К2, М2-И1-К3, М2-И1-К4, М2-И1-К5,
М2-И2-К1, М2-И2-К2, М2-И2-К3, М2-И2-К4, М2-И2-К5,
М2-И3-К1, М2-И3-К2, М2-И3-К3, М2-И3-К4, М2-И3-К5,
М2-И4-К1, М2-И4-К2, М2-И4-К3, М2-И4-К4, М2-И4-К5.
2 способ. Используя правило умножения, получаем: 2х4х5= 40.
Ответ: 40 вариантов.
3. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?
1 способ. Перечислим возможные варианты:
2 способ. Используя правило умножения, получаем: 5х3=15.
4. Мисс Марпл, расследуя убийство, заметила отъезжающее от дома мистера Дэвидсона такси. Она запомнила первую цифру “2”. В городке номера машин были трехзначные и состояли из цифр 1, 2, 3, 4 и 5. Скольких водителей, в худшем случае, ей придется опросить, чтобы найти настоящего убийцу?
1 способ. Перечислим возможные варианты номеров такси:
Ответ: 25 человек.
2 способ. Используя правило умножения, получаем: 5х5=25.
5. Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения?
1 способ. Пронумеруем стулья, на которых должен сесть каждый, и будем считать, что они рассаживаются поочередно:
№1 - Саша - есть возможность выбрать из 5 вариантов (стульев);
№2 - Петя - 4 варианта;
№3 - Денис - 3 варианта;
№4 - Оля - 2 варианта;
№5 - Настя- 1 вариант.
Используя правило умножения, получаем:  .
.
2 способ. Решаем, используя понятие факториала:  .
.
Ответ: 120 дней.
6. Из учащихся пяти 11 классов нужно выбрать двоих дежурных. Сколько пар дежурных можно составить (ученики в паре не должны быть из одного класса)?
1 способ. Перечислим возможные варианты состава пары:
11А-11Б, 11А-11В, 11А-11Г, 11А-11Д,11Б-11В, 11Б-11Г, 11Б-11Д, 11В-11Г, 11В-11Д, 11Г-11Д.
2 способ. Из пяти классов нужно выбрать 2 дежурных.
Число элементарных событий равно: 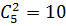 .
.
Ответ: 10 пар.
7. В 8 «а» классе лучше всех математику знают 5 учеников: Вася, Дима, Олег, Катя и Аня. На олимпиаду по математике нужно отправить пару, состоящую из 1 мальчика и 1 девочки. Сколькими способами учительница может эту пару выбрать?
1 способ. Обозначим имена детей первыми заглавными буквами.
Получаем следующие пары: В-К, В-А, Д-К, Д-А, О-К, О-А.
2 способ. Мальчиков 3, из них 1 можно выбрать  , девочек 2, из них можно 1 выбрать
, девочек 2, из них можно 1 выбрать  , используя правило умножения, получаем:
, используя правило умножения, получаем: 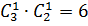 .
.
Ответ: 6 пар.
8. В соревнованиях по фигурному катанию принимали участие россияне, итальянцы, украинцы, немцы, китайцы и французы. Сколькими способами могут распределится места по окончании соревнований?
1 способ. Обозначим участников по первой заглавной букве страны и пронумеруем: Р1, И2, У3, Н4,К5, Ф6.
Р1 - имеют возможность занять с1-6 места, т.е. 6 вариантов;
И2 - 5 вариантов;
У3- 4 варианта;
Н4- 3 варианта;
К5- 2 варианта;
Ф6- 1 вариант.
Используя правило умножения, получаем:  .
.
2 способ. Используя понятие факториала, получаем:  .
.
Ответ: 720 способ.
9. В 9 «б» классе 6 человек (Галя, Света, Катя, Оля, Максим, Витя) учатся на все пятерки. Департамент образования премировал лучших учащихся путевками в Анапу. Но, к сожалению, путевок всего четыре. Сколько возможно вариантов выбора учеников на отдых?
1 способ. Обозначим первыми заглавными буквами имен учащихся.
Возможны следующие тройки:
Г-С-К-О, Г-С-К-М, Г-С-К-В,
Г-С-О-М, Г-С-О-В, Г-С-М-В
С-К-О-М, С-К-О-В, С-К-М-В,
К-О-М-В, С-О-М-В, Г-К-О-В,
Г-К-О-В, Г-О-М-В, Г-К-М-В.
2 способ. Из 6 человек нужно выбрать 4; число событий равно:  .
.
Ответ: 15 вариантов.
10. Пете на день рождения подарили 7 новых дисков с играми, а Вале папа привез 9 дисков из командировки. Сколькими способами они могут обменять 4 любых диска одного на 4 диска другого?
Вычислим, сколько четверок из 7 дисков можно составить у Пети:  , число четверок у Вали из 9 дисков -
, число четверок у Вали из 9 дисков -  .
.
По правилу умножения находим число обменов:  .
.
Ответ: 4410 способ.
11. Войсковое подразделение состоит из 5 офицеров, 8 сержантов и 70 рядовых. Сколькими способами можно выделить отряд из 2 офицеров, 4 сержантов и 15 рядовых?
Из 5 офицеров выбрать 2 можно с помощью числа сочетаний 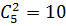 способами, из 8 сержантов 4 -
способами, из 8 сержантов 4 -  , из 70 рядовых 15 -
, из 70 рядовых 15 -  . По правилу умножения находим число выбора отряда:
. По правилу умножения находим число выбора отряда:
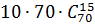 =
= 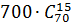 .
.
12. В ювелирную мастерскую привезли 6 изумрудов, 9 алмазов и 7 сапфиров. Ювелиру заказали браслет, в котором 3 изумруда, 5 алмазов и 2 сапфиров. Сколькими способами он может выбрать камни на браслет?
Из 6 изумрудов 3 он может выбрать 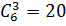 способами, из 9 алмазов 5 -
способами, из 9 алмазов 5 -  , из 7 сапфиров 2 -
, из 7 сапфиров 2 - 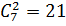 .
.
По правилу умножения находим число вариантов: 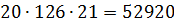 .
.
Ответ: 52920.
13. На выборах победили 9 человек - Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев, Володин, Афонин, Титов. Из них нужно выбрать председателя, заместителя и профорга. Сколькими способами это можно сделать?
Здесь речь идет о размещениях:  .
.
Можно было решать по-другому. На должность председателя выбираем из 9 человек, на заместителя - из 8, на профорга - из 7.
По правилу умножения получаем: 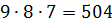 .
.
Ответ: 504.
14. В районе построили новую школу. Из пришедших 25 человек, устраиваться на работу, нужно выбрать директора школы, завуча начальной школы, завуча среднего звена и завуча по воспитательной работе. Сколькими способами это можно сделать?
На должность директора выбираем из 25 человек, на завуча начальной - из 24, завуча среднего звена - из 23, завуча по воспитательной работе - 22. По правилу умножения получаем:  .
.
Или, зная формулу размещения, получаем: 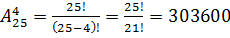 .
.
Ответ: 303600.
15. В студенческом общежитии в одной комнате живут трое студентов Петя, Вася и Коля. У них есть 6 чашек, 8 блюдец и 10 чайных ложек (все принадлежности отличаются друг от друга). Сколькими способами ребята могут накрыть стол для чаепития (так, что каждый получит чашку, блюдце и ложку)?
Для Пети набор можно набрать  способами, для Васи -
способами, для Васи -  , для Коли -
, для Коли -  . По правилу умножения получаем:
. По правилу умножения получаем:  способами.
способами.
Ответ: 29030400.
16. В кабинете заведующего ювелирного магазина имеется код, состоящий из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать мошеннику, чтобы раздобыть драгоценности, которые там хранятся?
В русском языке 9 гласных букв - а, е, е, и, о, у, э, ю, я. Выбрать из них 2 можно  способами. Из 10 цифр выбрать 3 можно
способами. Из 10 цифр выбрать 3 можно  способами. Применяя правило умножения, получаем:
способами. Применяя правило умножения, получаем:  .
.
Ответ: 4320.
17. Сколькими способами можно составить трехцветный флаг из горизонтальных полос разной ширины, если имеются материи из 8 тканей?
Эта задача на размещение:  .
.
Другой способ решения:
1цвет выбирается из 8 тканей 8 способами;
2цвет выбирается 7 способами;
3 цвет - 6способами.
Используя правило умножения, получаем:  способов.
способов.
Ответ: 336.
18. В 9 классе 15 предметов. Завучу школы нужно составить расписание на субботу, если в этот день 5 уроков. Сколько различных вариантов расписания можно составить, если все уроки различные?
Из 15 предметов 5 любых можно выбрать:  .
.
Ответ: 3003.
19. В огороде у бабушки растут 3 белые, 2 алые и 4 чайных розы. Сколькими различными способами можно составить букет из трех роз разного цвета?
1 способ. Обозначим белые - Б1, Б2, Б3, алые - А1, А2, чайные - Ч1, Ч2, Ч3,Ч4.
Перечислим возможные варианты:
Б1-А1-Ч1, Б1-А1-Ч2, Б1-А1-Ч3, Б1-А1-Ч4, Б1-А2-Ч1,Б1-А2-Ч2, Б1-А2-Ч3, Б1-А2-Ч4
Б2- А1-Ч1, Б2-А1-Ч2, Б2-А1-Ч3, Б2-А1-Ч4, Б2-А2-Ч1,Б2-А2-Ч2, Б2-А2-Ч3, Б2-А2-Ч4
Б3- А1-Ч1, Б3-А1-Ч2, Б3-А1-Ч3, Б3-А1-Ч4, Б3-А2-Ч1,Б3-А2-Ч2, Б3-А2-Ч3, Б3-А2-Ч4
2 способ. Используя правило умножения, получаем:  .
.
Ответ: 24 варианта.
20. К 60-летию Победы группа школьников отправилась по местам боевых действий в Смоленской области. Они планировали осуществить поход по маршруту деревни Сосновка - Быковка – Масловка- Видово. Из С в Б можно проплыть по реке или пройти пешком, из Б в М - пешком или на автобусе, из М в В - по реке, пешком или автобусе. Сколько вариантов похода есть у школьников?
Обозначим СБ - путь из Сосновки в Бытовку, ВГ - путь из Быковки в Масловку, МВ - путь из Масловки в Видово.
По реке - Р, пешком - П, на автобусе – А.
Перечислим возможные варианты:
СБР – БМП - МВР, СБР – БМП - МВП, СБР – БМП - МВА
СБР – БМА - МВР, СБР – БМА - МВП, СБР – БМА - МВА
СБА – БМП - МВР, СБА – БМП - МВП, СБА – БМП - МВА
СБА – БМА - МВР, СБА – БМА - МВП, СБА – БМА – МВА
Ответ: 12 вариантов.
Не нашли, что искали? Воспользуйтесь поиском: