Закрепление изученного материала.

Самостоятельное решение задач с последующей проверкой.

Вариант 1. 1. Какой фигурой является сечение куба А…D1 плоскостью, проходящей через вершины В1 и середину ребра СС1? 2. Постройте сечение куба плоскостью, проходящей через три точки, расположенные так, как показано на рисунке.

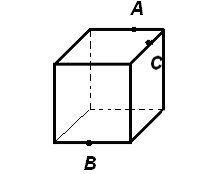
Вариант 2. 1. Какой фигурой является сечение куба А…D1 плоскостью, проходящей через середины ребер АВ, ВС, и DD1? 2. Постройте сечение куба плоскостью, проходящей через три точки, расположенные так, как показано на рисунке.

Вопросы для самоконтроля:

1. В каком случае в сечение куба получается треугольник (равносторонний, равнобедренный, разносторонний)?

2. Какие четырехугольники могут получится в сечении куба плоскостью?

3. Может ли в сечении куба плоскостью получится правильный пятиугольник? Почему?

4. В каком случае в сечении куба плоскостью получится правильный шестиугольник?

5. Может ли в сечении куба получится четырехугольник изображенный на рисунке?

6. В чем заключается построение сечений методом «следов»?

Решить задачу:

Построить сечение куба плоскостью проходящей через точки М, N, К.

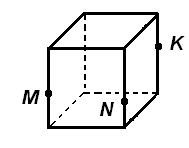
Рекомендуемая литература:

Основные источники:

1. Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.

2. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

4. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

5. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

Дополнительные источники:

1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

4. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

5. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

6. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

7. Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.

8. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

9. Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.

10. Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.

11. Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.

12. Пехлецкий И.Д. Математика: учебник. – М., 2003.

13. Смирнова И.М. Геометрия. 10 (11) кл. – М., 2000.

Интернет ресурсы:

1. Колмогоров А.Н. (ред.) — Алгебра и начала анализа: Электронная книга. Lib.mexmat.ru/books/3307

2. Алгебра и начала анализа. 10-11 класс. Учебник. Мордкович

e-ypok.ru/content/

3. «Математика для колледжей» Математический Портал – библиотека math-portal.ru

Не нашли, что искали? Воспользуйтесь поиском: