ДЕСЯТИЧНЫЕ И НАТУРАЛЬНЫЕ ЛОГАРИФМЫ

Среди других оснований логарифмов весьма удобны для вычислений десятичные логарифмы - логарифмы при основании 10. Это связано с тем, что мы пользуемся десятичной системой счисления. Десятичные логарифмы даже обозначаются особым знаком .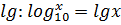

Но есть такое основание логарифмов, которое объективно удобнее остальных для вычислений. Самое удобное для вычислений - когда функция и аргумент изменяются примерно одинаково. Именно таким является логарифм, график которого пересекает ось абсцисс в точке 1 под углом 45°. Ученые назвали такой логарифм натуральным и обозначили его основание буквой е в честь Леонарда Эйлера.

Натуральные логарифмы обозначаются сокращенной формулой : 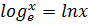. Достаточно помнить, что е =2,7….

Решите:

1. Исследуйте и построите графики следующих функций:

; ; ; .

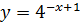2. Исследуйте и построите графики следующих функций:

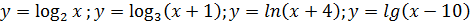
Вопросы для самоконтроля:

1. Что такое показательная функция?

2. Как записывается показательная функция?

3. Что такое основание показательной функций?

4. Перечислите основные свойства показательной функций.

5. Что такое логарифмическая функция?

6. Как записывается логарифмическая функция?

7. Что такое основание логарифмической функций?

8. Перечислите основные свойства логарифмической функций.

Рекомендуемая литература:

Основные источники:

1. Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.

2. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

4. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

5. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

Дополнительные источники:

1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

4. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

5. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

6. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

7. Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.

8. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

Интернет ресурсы:

1. Колмогоров А.Н. (ред.) — Алгебра и начала анализа: Электронная книга. Lib.mexmat.ru/books/3307

2. Алгебра и начала анализа. 10-11 класс. Учебник. Мордкович

e-ypok.ru/content/

3. «Математика для колледжей» Математический Портал – библиотека math-portal.ru

Не нашли, что искали? Воспользуйтесь поиском: