
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Свойства показательной функции
| Свойства показательной функции | y = a x, a > 1 | y = a x, 0< a < 1 |
| 1. Область определения функции | 
| |
| 2. Область значений функции | 
| |
| 3.Промежутки сравнения с единицей | при x > 0, a x >1 | при x > 0, 0< a x < 1 |
| при x < 0, 0< a x < 1 | при x < 0, a x >1 | |
| 4. Чётность, нечётность. | Функция не является ни чётной, ни нечётной (функция общего вида). | |
| 5.Монотонность. | монотонно возрастает на R | монотонно убывает на R |
| 6. Экстремумы. | Показательная функция экстремумов не имеет. | |
| 7.Асимптота | Ось O x является горизонтальной асимптотой. | |
8. При любых действительных значениях x и y; 
| 
|
Когда заполняется таблица, то параллельно с заполнением решаются задания.
Задание № 1. (Для нахождения области определения функции).
Какие значения аргумента являются допустимыми для функций:

Задание № 2. (Для нахождения области значений функции).
На рисунке изображен график функции. Укажите область определения и область значений функции:

| 
|

| 
|
Задание № 3. (Для указания промежутков сравнения с единицей).
Каждую из следующих степеней сравните с единицей:
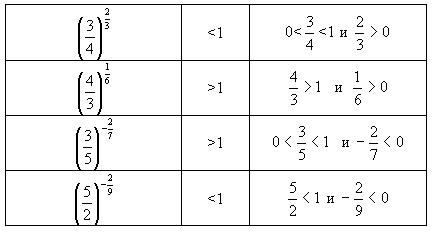
Задание № 4. (Для исследования функции на монотонность).
Сравнить по величине действительные числа m и n если:

Задание № 5. (Для исследования функции на монотонность).
Сделайте заключение относительно основания a, если:

В одной координатной плоскости построены графики функций:
y(x) = 10x; f(x) = 6x; z(x) - 4x
Как располагаются графики показательных функций относительно друг друга при x > 0, x = 0, x < 0?

Вывод:
| при x < 0 | чем больше значение основания степени, тем ближе к оси O x располагается график показательной функции; |
| при x = 0 | графики показательных функций пересекаются в одной точке (0;1); |
| при x > 0 | чем больше значение основания степени, тем дальше от оси O x располагается график показательной функции. |
В одной координатной плоскости построены графики функций:
y(x) = (0,1)x; f(x) = (0,5)x; z(x) = (0,8)x.
Как располагаются графики показательных функций относительно друг друга при x > 0, x = 0, x < 0?

Вывод:
| при x < 0 | чем меньше значение основания степени, тем дальше от оси O x располагается график показательной функции; |
| при x = 0 | графики показательных функций пересекаются в одной точке (0;1); |
| при x > 0 | чем меньше значение основания степени, тем ближе к оси O x располагается график показательной функции. |
Число  одна из важнейших постоянных в математике. По определению, оно равно пределу последовательности одна из важнейших постоянных в математике. По определению, оно равно пределу последовательности 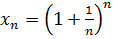 при неограниченномвозрастании n. Обозначение e ввёл Леонард Эйлер в 1736 г. Он вычислил первые 23 знака этого числа в десятичной записи, а само число назвали в честь Непера «неперовым числом».
Число e играет особую роль в математическом анализе. Показательная функция с основанием e, называется экспонентой и обозначается y = ex.
Первые знаки числа e запомнить несложно: два, запятая, семь, год рождения Льва Толстого - два раза, сорок пять, девяносто, сорок пять. при неограниченномвозрастании n. Обозначение e ввёл Леонард Эйлер в 1736 г. Он вычислил первые 23 знака этого числа в десятичной записи, а само число назвали в честь Непера «неперовым числом».
Число e играет особую роль в математическом анализе. Показательная функция с основанием e, называется экспонентой и обозначается y = ex.
Первые знаки числа e запомнить несложно: два, запятая, семь, год рождения Льва Толстого - два раза, сорок пять, девяносто, сорок пять.
|
Логарифмическая функция - функция, обратная показательной функции.
Чтобы получить формулу логарифмической функции, напишем формулу показательной функции  , выразим х через у и поменяем обозначения переменных:
, выразим х через у и поменяем обозначения переменных:

В этой формуле число а - то самое, которое является основанием показательной функции. То есть а обязательно положительное число, не равное единице.
Теперь можно дать и другое определение: Логарифмической функцией называется функция, которую можно задать формулой  , где а - положительное число, не равное единице.
, где а - положительное число, не равное единице.
Не нашли, что искали? Воспользуйтесь поиском: