Рассмотрим теперь вопрос о построении сечений куба.

Решение примеров и задач (алгоритм выполнения задания):

Задача: Пусть дано изображение куба и три точки А, В, С, принадлежащие ребрам этого куба, выходящим из одной вершины.

Решение: Чтобы построить сечение куба плоскостью, проходящей через эти точки, достаточно просто соединить их отрезками. Полученный треугольник АВС и будет искомым изображением сечения куба.

Для построения более сложных сечений используют метод «следов», заключающийся в нахождении точки пересечения прямой и плоскости по заданным двум точкам этой прямой и их проекциям на плоскость.

Задача №1. Пусть прямая проходит через точки А, В и известны параллельные проекции А′,В′ этих точек на плоскости π. Требуется найти точку пересечения прямой АВ с плоскостью π.

Решение: Через точки А′,В′ проведем прямую k′.
Пересечение прямой k с k′ и будет искомым пересечением прямой k с плоскостью π.

Задача № 2. Даны точки А,В,С и их параллельные проекции А′, В′, С′ на плоскость π.Требуется построить линию пересечения плоскости АВС и плоскости π.
Решение: Построить точки Х и У пересечения прямых АВ и АС с плоскостью π.Прямая ХУ будет искомой линией пересечения плоскости АВС и плоскости π.

Задача №3. Через данную точку С (С′) провести прямую, параллельную данной прямой АВ (А′В′), и найти ее точку пересечения с плоскостью π.
Решение: Через точку С проведем прямую, параллельную АВ. Через точку С′ проведем прямую, параллельную А′ В′. Точка Х пересечения этих прямых и будет искомой.

Используя этот метод, решим задачу на построение сечения куба.

Задача №4. Построить сечение куба плоскостью, проходящей через три точки А, В, С, принадлежащие попарно скрещивающимся ребрам этого куба.
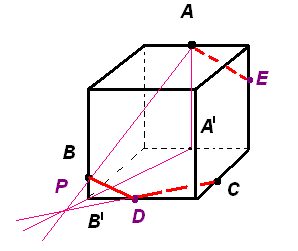
Решение: Найдем пересечение прямой АВ, лежащей в плоскости сечения, с плоскостью основания куба. Для этого построим параллельные проекции А′, В′ точек А, В на основании куба в направлении бокового ребра куба.

Пересечение прямых АВ и А′В′ будет искомой точкой Р. Она принадлежит плоскости сечения и плоскости основания куба. Следовательно, плоскость сечения пересекает основание куба по прямой СР.

Точка пересечения этой прямой с ребром основания куба даст еще одну точку D сечения куба. Соединим точки С и D, B и D отрезками.

Через точку А проведем прямую, параллельную ВD, и точку ее пересечения с ребром кубам обозначим Е.

Соединим точки Е и С отрезком.

Через точку А проведем прямую, параллельную СD, и точку ее пересечения с ребром куба обозначим F.

Соединим точки В и F отрезком.

Многоугольник AECDBF и будет искомым изображением сечения куба плоскостью.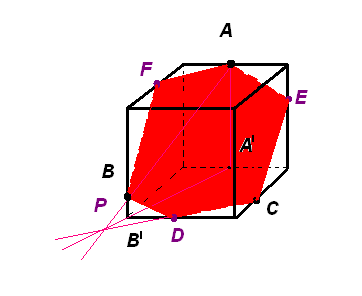

Не нашли, что искали? Воспользуйтесь поиском: