Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица такова, что если матрицу умножить на обратную ей матрицу, то получится единичная матрица:

Обратная матрица существует не всегда. Матрицы, для которых обратная матрица существует, называются невырожденными (или регулярными), а для которых нет — вырожденными(или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.

4. Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы[

· , где обозначает определитель.

· для любых двух обратимых матриц и .

· где обозначает транспонированную матрицу.

· для любого коэффициента .

· Если необходимо решить систему линейных уравнений , (b — ненулевой вектор) где — искомый вектор, и если существует, то . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

5. Системы линейных уравнений[править | править исходный текст]

Основная статья: Система линейных алгебраических уравнений

Рассмотрим систему линейных уравнений вида:

.

Эта система состоит из линейных уравнений относительно неизвестных, может быть записана в виде следующего матричного уравнения вида:

,

где

Матрица — это матрица коэффициентов системы линейных уравнений, вектор-столбец — вектор неизвестных, а вектор-столбец — некоторый заданный вектор.

Для того, чтобы система имела решение (хотя бы одно), необходимо и достаточно, чтобы вектор был линейной комбинацией столбцов , и тогда вектор — это вектор, содержащий коэффициенты разложения вектора по столбцам матрицы .

На языке матриц условие разрешимости системы линейных уравнений формулируется в виде теоремы Кронекера-Капелли:

ранг матрицы равен рангу расширенной матрицы .

В том случае, когда количество уравнений совпадает с количеством неизвестных (), матрица квадратная, и условие разрешимости соответствующей системы уравнений оказывается равносильным условию невырожденности матрицы .

Тогда решение системы следует искать в виде

,

что очевидным образом приводит к алгоритму вычисления значений неизвестных переменных по правилу Крамера.

Линейные преобразования[править | править исходный текст]

Основная статья: Линейное отображение

Рассмотрим линейное преобразование , действующее из -мерного векторного пространства в -мерное векторное пространство , имеющее следующий вид:

.

В матричной форме это преобразование уравнения вида:

.

Матрица — это матрица коэффициентов линейного преобразования.

Если рассмотреть действие линейного преобразования на векторы вида

,

составляюще базис пространства , то — это есть j -ый столбец матрицы .

Таким образом, матрица полностью описывает линейное преобразование , и, поэтому, называется матрицей линейного преобразования.

6. Если к квадратной матрице дописать справа единичную матрицу того же порядка и с помощьюэлементарных преобразований над строками добиться того, чтобы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной.

7. формула крамера

Описание метода

Для системы линейных уравнений с неизвестными (над произвольным полем)

с определителем матрицы системы , отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы и , либо набор состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Пример

Система линейных уравнений:

Определители:

Решение:

Пример:

Определители:

Метод Гаусса

Пусть исходная система выглядит следующим образом

Матрица называется основной матрицей системы, — столбцом свободных членов.

Тогда, согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных ^[3].

Тогда переменные называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число , где , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.

Пусть для любых .

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (, где — номер строки):

,
где

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Пример

Покажем, как методом Гаусса можно решить следующую систему:

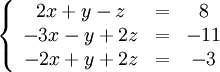
Обнулим коэффициенты при во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на и , соответственно:

Теперь обнулим коэффициент при в третьей строке, вычтя из неё вторую строку, умноженную на :

В результате мы привели исходную систему к треугольному виду, тем самым закончим первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

из третьего;

из второго, подставив полученное

из первого, подставив полученные и .

Таким образом исходная система решена.

В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.

Не нашли, что искали? Воспользуйтесь поиском: