Последовательность на бесконечности

Последовательность имеет бесконечный предел, если для любого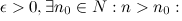

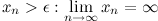
Последовательность называется бесконечно малой, если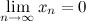

Последовательность называется бесконечно большой, если для любого существует номер такое, что для любого

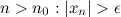
Теорема

Пусть 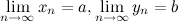, тогда

а) ;

б) ;

в) если , то начиная с некоторого номера заданная последовательность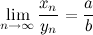

20. Предел функции в точке и на бесконечности.
Пусть функция определена на некотором множестве Х и пусть точка. Возьмем из Х последовательность точек, отличных от х₀:

х₁, х₂, х₃,…, х_n,…, (1)

Сходящиеся к х₀ (предполагается, что такая последовательность существует). Значения функции в точках этой последовательности также образуют числовую последовательность

(2)

и можно ставить вопрос о существовании её предела.
Определение1. Число А называется пределом функции 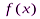в точке x=х₀ (или при 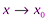), если для любой сходящейся к х₀ последовательности (1) значении аргумента x, отличных от х₀, соответствующая последовательность (2) значений функции сходится к числу А. Обозначается .

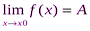Функция 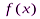может иметь в точке х₀ только один предел. Это следует из того, что последовательность 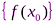имеет только один предел.

Примеры.

1). Функция 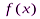=с=const имеет предел в каждой точке х₀ числовой прямой, т.е.

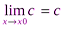
2). Функция 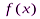= x имеет в любой точке х₀ числовой прямой предел, равный х₀, т.е.

Определение 2. Число А называется пределом функции в точке х=х₀, если для любого числа существует число 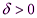такое, что для всех 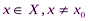, удовлетворяющих неравенству 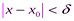, выполняется неравенство .
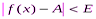Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением ''на языке последовательностей'', или определением по Гейне (1821-1881 – немецкий математик). Второе определение называют определение м ''на языке '', или определением по Коши (1789-1857 – французский математик).

Можно доказать, что оба определения предела функции в точке х₀ эквивалентны, а это значит, что можно использовать любое из них в зависимости от того какое более удобно при решении той или иной задачи.

Кроме рассмотренного понятия предела функции при существует также понятие предела функции при .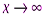
Определение. Число А называется пределом функции при , если для любого ^ Е>0 можно указать такое положительное число N, что для всех значений x, удовлетворяющих неравенству , будет выполнятся неравенство .

Не нашли, что искали? Воспользуйтесь поиском: