
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Относительная частота, статистическое определение вероятности.
Относительной частотой события А называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний:
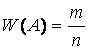 ,
,
где m – число появлений события А, n – общее число испытаний.
Классическая вероятность вычисляется до опыта, а относительная частота – после опыта.
Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число и есть вероятность появления события.
Таким образом, при достаточно большом количестве испытаний в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.
.
3. Классическое определение вероятности.
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Итак, вероятность события А определяется формулой:
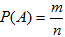
где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.
Из определения вероятности вытекают следующие ее свойства:
Свойство 1. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m=n, следовательно, P(A)=m/n=n/n=1
Свойство 2. Вероятность невозможного события равна нулю.
В этом случае m=0, следовательно, P(A)=m/n=0/n=0
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит 0<m/n<1, следовательно,
0<P(A)<1
Итак, вероятность любого события удовлетворяет двойному неравенству
0  P(A)
P(A)  1
1
4. Геометрическое определение вероятности, задача о встрече.
Пусть пространство элементарных событий служит множество точек некоторой области G, имеющей площадь на плоскости. В качестве событий будем рассматривать площадь подмножества А, В, С,... этой области. При этом вероятность любого события А (подмножества, имеющего площадь mes (A)), можно задать следующим образом:
 .(
.( - мера)
- мера)
Например: Пусть отрезок длиной l включается в отрезок длиной L. Вероятность события А «наудачу брошенная точка попала на отрезок длиной l» определяется равенством
| P(A)= | длина отрезка l | |
| длина отрезка L |
Пусть плоская фигура площадью s включается в плоскую фигуру площадью S. Вероятность события А«наудачу брошенная точка попала на плоскую фигуру площадью s» определяется равенством
| P(A)= | площадь s | |
| площадь S |
Пусть пространственная фигура объемом v включается в пространственную фигуру объемом V. Вероятность события А «наудачу брошенная точка попала на пространственную фигуру объемом v» определяется равенством
| P(A)= | объём v | |
| объём V |
Задача о встрече. Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?
Решение: Используем геометрическое определение вероятности события A = (Встреча с другом состоится).
Обозначим за х и у время прихода, 0≤х,у≤60 (минут). В прямоугольной системе координат этому условию удовлетворяют точки, лежащие внутри квадрата ОАВС. Друзья встретятся, если между моментами их прихода пройдет не более 5 минут, то есть
y − x <5, y > x,
x − y <5, x > y.
Этим неравенствам удовлетворяют точки, лежащие в области G, очерченной красным.

Тогда вероятность встречи равна отношению площадей области G и квадрата, то есть
P (A)= SGSOABC =60⋅60−55⋅5560⋅60=23144=0,16.
Ответ: 0,16
5. Аксиоматическое определение вероятности
Будем считать, что относительно событий из рассматриваемого поля справедливы следующие высказывания:
Аксиома 1. Каждому случайному событию A ставится в соответствие неотрицательное число p, p=P(A), называемое вероятностью события A.
Аксиома 2. Вероятность достоверного события равна единице, т.е. P(D)=1.
Аксиома 3. (аксиома сложения). Вероятность суммы конечного числа попарно несовместных событий, равна сумме вероятностей этих событий, т. е.
P(A  +A
+A  + …+A
+ …+A  )=P(A
)=P(A  )+P(A
)+P(A  )+…+P(A
)+…+P(A  ), если A
), если A  A
A  =N при всех i
=N при всех i  k.
k.
Такое определение вероятности называется аксиоматическим. Из аксиоматического определения следуют следующие свойства вероятности: 1) P(N)=0; 2) P( )=1-P(A); 3) 0
)=1-P(A); 3) 0  P(A)
P(A)  1; 4) P(B)
1; 4) P(B)  P(A), если A
P(A), если A  B; 5) P(A)=P(B), если A=B.
B; 5) P(A)=P(B), если A=B.
6. Формулы комбинаторики.
Комбинаторика – раздел математики, изучающий, в частности, методы решения комбинаторных задач, т. е. задач о подсчете числа различных комбинаций (выборок), получаемых из элементов заданного конечного множества.
Пусть 
 …,
…,  - элементы некоторого конечного множества. Сформулируем два важных правила, часто применяемых при решении комбинаторных задач.
- элементы некоторого конечного множества. Сформулируем два важных правила, часто применяемых при решении комбинаторных задач.
Правило суммы. Если элемент  может быть выбран
может быть выбран  способами, элемент
способами, элемент  - другими
- другими  способами,
способами,  - отличными от первых двух
- отличными от первых двух  способами и т.д.,
способами и т.д.,  -
-  способами, отличными от первых (k-1), то выбор одного из элементов: или
способами, отличными от первых (k-1), то выбор одного из элементов: или  или
или  …, или
…, или  может быть осуществлен
может быть осуществлен  способами.
способами.
Правило произведения (основной принцип). Если элемент  может быть выбран
может быть выбран  способами, после каждого такого выбора элемент
способами, после каждого такого выбора элемент  может быть выбран
может быть выбран  способами и т.д., после каждого (k-1) выбора элемент
способами и т.д., после каждого (k-1) выбора элемент  может быть выбран
может быть выбран  способами, то выбор всех элементов
способами, то выбор всех элементов 
 …,
…,  в указанном порядке может быть осуществлен
в указанном порядке может быть осуществлен  способами.
способами.
Приведем некоторые понятия и формулы, которые лежат в основе комбинаторики.
Пусть дано множество, состоящее из n различных элементов: 
 …,
…,  . Из этого множества могут быть образованы комбинации (выборки) из m элементов (0<m
. Из этого множества могут быть образованы комбинации (выборки) из m элементов (0<m  n).
n).
Размещениями из n элементов по m называются комбинации (выборки), состоящие из m элементов и отличающиеся друг от друга либо составом элементов, либо порядком их расположения (либо и тем и другим).
Число размещений из n элементов по m обозначается символом  (“A из эн по эм”) и вычисляется по формуле
(“A из эн по эм”) и вычисляется по формуле

или  , где
, где  ; 1!=1; 0!=1.
; 1!=1; 0!=1.
Перестановками из n элементов называются комбинации (выборки), состоящие из n элементов и отличающиеся друг от друга только порядком следования элементов.
Число перестановок из n элементов обозначается символом  (“пэ из эн”) и вычисляется по формуле
(“пэ из эн”) и вычисляется по формуле

Сочетаниями из n элементов по m (0<m  n) называются комбинации (выборки), состоящие из m элементов, взятых из данных n элементов, и отличающиеся друг от друга хотя бы одним элементом, т. е. отличающиеся только составом элементов.
n) называются комбинации (выборки), состоящие из m элементов, взятых из данных n элементов, и отличающиеся друг от друга хотя бы одним элементом, т. е. отличающиеся только составом элементов.
Число сочетаний из n элементов по m обозначается символом  (“цэ из эн по эм”) и вычисляется по формуле:
(“цэ из эн по эм”) и вычисляется по формуле:

или  .
.
Так как по определению  , то
, то  .
.
7. Теоремы сложения.
Вероятность суммы конечного числа попарно несовместных событий определяется аксиомой 3 (аксиомой сложения вероятностей).
При решении ряда задач требуется найти вероятность суммы двух или нескольких совместных событий, т.е. вероятность появления хотя бы одного из этих событий. В этом случае аксиома сложения вероятностей не применима.
Теорема (правило) сложения вероятностей. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения, т. е.
 (8)
(8)
В случае трех и более совместных событий соответствующая формула для вероятности суммы событий  весьма громоздка, проще перейти к противоположному событию
весьма громоздка, проще перейти к противоположному событию  и затем воспользоваться равенством
и затем воспользоваться равенством  . Тогда
. Тогда
 , (9)
, (9)
т. е. вероятность суммы нескольких совместных событий  равна разности между единицей и вероятностью произведения противоположных событий
равна разности между единицей и вероятностью произведения противоположных событий  .
.
Если при этом события  независимые, то
независимые, то
 (10)
(10)
8. Независимые события, теоремы умножения.
Условной вероятностью события A по отношению к событию B называется вероятность события A, найденная при условии, что событие B произошло. Обозначается символом  .
.
События A и B называются независимыми, если появление одного из них не меняет вероятность появления другого, т. е. если
 ,
,  .
.
Теорема (правило) умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого, найденную в предположении, что первое событие произошло, т.е.
 или
или  (4)
(4)
Теорема умножения вероятностей для нескольких событий. Вероятность произведения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности остальных событий, вычисленные в предположении, что все предыдущие события произошли, т. е.
 . (5)
. (5)
Для независимых событий  и
и  правило умножения вероятностей принимает вид:
правило умножения вероятностей принимает вид:
 (6)
(6)
Эта формула часто используется в качестве определения независимых событий.
События  называются независимыми (или независимыми в совокупности), если вероятность любого из них не меняется от того, что произошло одно или несколько других событий, т. е.
называются независимыми (или независимыми в совокупности), если вероятность любого из них не меняется от того, что произошло одно или несколько других событий, т. е.
 , где
, где  .
.
В случае n независимых событий имеем
 , (7)
, (7)
т.е. вероятность произведения двух или нескольких независимых событий равна произведению вероятностей этих событий.
События  называются попарно - независимыми, если любые два события
называются попарно - независимыми, если любые два события  и
и  (
( ) из этого набора независимы.
) из этого набора независимы.
Независимые события  являются попарно – независимыми. Обратное, вообще говоря, неверно.
являются попарно – независимыми. Обратное, вообще говоря, неверно.
9. Повторение испытаний. Формула Бернулли.
Пусть производится n независимых испытаний, в каждом из которых может произойти некоторое событие A с одной и той же вероятностью P(A)=p или произойти противоположное событие  с вероятностью
с вероятностью  (такого рода схема испытаний называется схемой Бернулли). Тогда вероятность того, что событие A наступит в этих n испытаниях ровно m раз находится по формуле Бернулли
(такого рода схема испытаний называется схемой Бернулли). Тогда вероятность того, что событие A наступит в этих n испытаниях ровно m раз находится по формуле Бернулли
 , m = 0,1,2,…,n, где
, m = 0,1,2,…,n, где  (13)
(13)
Формула (13) выражает так называемое биномиальное распределение.
Из формулы Бернулли, в частности, следует, что вероятность того, что в n испытаниях, удовлетворяющих схеме Бернулли, событие A наступит не менее  раз, равна
раз, равна  или
или  .
.
Вероятность наступления события A хотя бы один раз в n испытаниях равна
 . (14)
. (14)
Число  (
( ) называется наивероятнейшим числом наступлений события A в схеме Бернулли, если
) называется наивероятнейшим числом наступлений события A в схеме Бернулли, если  для всех m=0,1,2,…,n. Если вероятности p и q отличны от нуля, то число
для всех m=0,1,2,…,n. Если вероятности p и q отличны от нуля, то число  определяется из двойного неравенства
определяется из двойного неравенства
 . (15)
. (15)
Разность граничных значений в этом двойном неравенстве равна 1. Если  не является целым числом, то двойное неравенство определяет лишь одно наивероятнейшее значение
не является целым числом, то двойное неравенство определяет лишь одно наивероятнейшее значение  .
.
Если же  - целое число, то имеются два наивероятнейших значения:
- целое число, то имеются два наивероятнейших значения:  и
и  .
.
10. Наивероятнейшее число событий.
11. Формула полной вероятности. Формулы Байеса.
Вероятность P(B) появления события B, которое может произойти только совместно с одним из событий  , образующих полную группу попарно несовместных событий, т. е.
, образующих полную группу попарно несовместных событий, т. е.  и
и  , вычисляется по формуле полной вероятности
, вычисляется по формуле полной вероятности
 где
где  . (11)
. (11)
При этом события  обычно называют гипотезами, а числа
обычно называют гипотезами, а числа  - вероятностями гипотез.
- вероятностями гипотез.
Условная вероятность гипотезы  в предположении, что событие B уже имеет место, определяется по формуле Бейеса:
в предположении, что событие B уже имеет место, определяется по формуле Бейеса:
 , (
, ( ) (12)
) (12)
Вероятности  , вычисленные по формуле Бейеса, часто называют вероятностями гипотез.
, вычисленные по формуле Бейеса, часто называют вероятностями гипотез.
12. Случайные величины.
Случайной называют величину, которая в результате испытания примет случайно одно и только одно значение из множества возможных значений.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные возможные значения с определенными вероятностями.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
13. Функция распределения (интегральный закон распределения).
Функцией распределения (или интегральной функцией распределения) случайной величины X называется функция  , которая для любого числа
, которая для любого числа  равна вероятности события, состоящего в том, что случайная величина
равна вероятности события, состоящего в том, что случайная величина  примет значение, меньшее, чем
примет значение, меньшее, чем  , т. е.
, т. е.  .
.
Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее данной точки x (рис. 2).

Рис. 2
Функция F(x) существует как для дискретных, так и непрерывных случайных величин.
Функция распределения обладает следующими свойствами:
1.  ;
;
2.  - неубывающая функция, т. е.
- неубывающая функция, т. е.  , если
, если  ;
;
3.  ,
,  ;
;
4.  - непрерывна слева в любой точке x, т. е.
- непрерывна слева в любой точке x, т. е.  ,
,  ;
;
5.  .
.
Функция распределения дискретной случайной величины имеет вид:
 ,
,
где суммирование ведется по всем индексам  , для которых
, для которых  . Для дискретной случайной величиныфункция распределения есть разрывная ступенчатая функция, непрерывная слева.
. Для дискретной случайной величиныфункция распределения есть разрывная ступенчатая функция, непрерывная слева.
14. Плотность распределения (дифференциальный закон распределения).
Случайная величина X называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
В отличие от дискретных случайных величин вероятность отдельного значения для непрерывной случайной величины равна нулю:  . Поэтому для непрерывной случайной величины X имеем
. Поэтому для непрерывной случайной величины X имеем
 . (*)
. (*)
Для непрерывных случайных величин кроме функции распределения существует еще один удобный способ задания закона распределения – плотность вероятности.
Пусть функция распределения  данной непрерывной случайной величины X непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек.
данной непрерывной случайной величины X непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек.
Плотностью распределения непрерывной случайной величины X (или плотностью вероятности, или просто плотностью) называется функция  .
.
Функцию  называют также дифференциальной функцией распределения.
называют также дифференциальной функцией распределения.
Плотность распределения любой непрерывной случайной величины неотрицательна, т. е.  ; обладает свойством нормированности:
; обладает свойством нормированности:
 ;
;  .
.
График функции  называется кривой распределения.
называется кривой распределения.
Функция распределения F(x) выражается через плотность распределения формулой
 (1)
(1)
Вероятность попадания непрерывной случайной величины  в промежуток
в промежуток  определяется равенством:
определяется равенством:
 . (2)
. (2)
15. Математическое ожидание, его свойства.
Математическим ожиданием (или средним значением)  (или
(или  ) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.
) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.
Если дискретная случайная величина X принимает конечное число значений  , то ее математическое ожидание
, то ее математическое ожидание  находится по формуле
находится по формуле
 (3)
(3)
Если же дискретная случайная величина X принимает бесконечное (счетное) число значений, то
 , (4)
, (4)
при этом математическое ожидание существует, если ряд в правой части этой формулы абсолютно сходится, т. е. сходится ряд  .
.
Математическое ожидание непрерывной случайной величины X с плотностью вероятности  , находится по формуле
, находится по формуле
 , (5)
, (5)
при этом математическое ожидание существует, если интеграл в правой части равенства абсолютно сходится (это значит, что сходится интеграл  ).
).
16. Дисперсия, ее свойства, среднее квадратическое отклонение.
Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
Свойства дисперсии
1) Дисперсия постоянной величины равна нулю.
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
Справедливость этого равенства вытекает из свойства 2.
Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии.
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.
17. Мода и медиана.
Модой  дискретной случайной величины X называется ее наиболее вероятное значение.
дискретной случайной величины X называется ее наиболее вероятное значение.
Модой непрерывной случайной величины X называется такое ее значение  , при котором плотность распределения
, при котором плотность распределения  имеет максимум, т. е.
имеет максимум, т. е.  .
.
На рис. 3 и 4 показана мода для дискретной и непрерывной случайной величины.


Рис. 3 Рис. 4
Если многоугольник распределения (кривая распределения) имеет два или несколько максимумов, то распределение называется двухмодальным или многомодальным.
Иногда встречаются распределения, которые имеют минимум, но не имеют максимум. Такие распределения называются антимодальными.
Медианой непрерывной случайной величины X (обозначение:  ) называется такое ее значение
) называется такое ее значение  , для которого одинаково вероятно, окажется ли случайная величина
, для которого одинаково вероятно, окажется ли случайная величина  меньше
меньше  или больше
или больше  , т. е.
, т. е.
 . (9)
. (9)
Геометрически вертикальная прямая  , проходящая через точку с абсциссой, равной
, проходящая через точку с абсциссой, равной  , делит площадь фигуры под кривой распределения на две равные части (рис. 5). Каждая из этих площадей равна
, делит площадь фигуры под кривой распределения на две равные части (рис. 5). Каждая из этих площадей равна  , т. к. площадь, ограниченная кривой распределения, равна единице. Поэтому функция распределения в точке
, т. к. площадь, ограниченная кривой распределения, равна единице. Поэтому функция распределения в точке  равна
равна  , т. е.
, т. е.  .
.

Рис. 5
Для дискретной случайной величины медиана обычно не определяется.
18. Моменты случайных величин.
При обработке данных используют такие характеристики случайной величины Х как моменты порядка q, т.е. математические ожидания случайной величины Xq, q = 1, 2, … Так, само математическое ожидание – это момент порядка 1. Для дискретной случайной величины момент порядка q может быть рассчитан как

Для непрерывной случайной величины

Моменты порядка q называют также начальными моментами порядка q, в отличие от родственных характеристик – центральных моментов порядка q, задаваемых формулой

Так, дисперсия – это центральный момент порядка 2.
19. Производящая функция.
Производя́щая фу́нкция моме́нтов — способ задания вероятностных распределений.
Пусть есть случайная величина  с распределением
с распределением  . Тогда её производящей функцией моментов называется функция, имеющая вид:
. Тогда её производящей функцией моментов называется функция, имеющая вид:
 .
.
Пользуясь формулами для вычисления математического ожидания, определение производящей функции моментов можно переписать в виде:
 ,
,
то есть производящая функция моментов - это двустороннее преобразование Лапласа распределения случайной величины (с точностью до отражения).
Если случайная величина  дискретна, то есть
дискретна, то есть  , то
, то
 .
.
Свойства производящих функций моментов во многом аналогичны свойствам характеристических функций в силу похожести их определений.
· Производящая функция моментов однозначно определяет распределение. Пусть  суть две случайные величины, и
суть две случайные величины, и  . Тогда
. Тогда  . В частности, если обе величины абсолютно непрерывны, то совпадение производящих функций моментов влечёт совпадение плотностей. Если обе случайные величины дискретны, то совпадение производящих функций моментов влечёт совпадение функций вероятности.
. В частности, если обе величины абсолютно непрерывны, то совпадение производящих функций моментов влечёт совпадение плотностей. Если обе случайные величины дискретны, то совпадение производящих функций моментов влечёт совпадение функций вероятности.
· Производящая функция моментов как функция случайной величины однородна:
·  .
.
· Производящая функция моментов суммы независимых случайных величин равна произведению их производящих функций моментов.
20. Асимметрия и эксцесс.
Асимметрия – это показатель симметричности / скошенности кривой распределения, а эксцесс определяет ее островершинность.
При левостронней асимметрии ее показатель является положительным и в распределении преобладают более низкие значения признака. При правостронней – показатель положительный и преобладают более высокие значения. У всех симметричных распеделений (в том числе и у нормального распределения) величина асимметрии равна нулю. Формула показателя асимметрии является следующей:

Если в распределении преобладают значения близкие к среднему арифметическому, то формируется островершинное распределение. В этом случае показатель эксцесса стремится к положительной величине. У нормального распределения эксцесс равен нулю. Если у распределения 2 вершины (бимодальное распределение), то тогда эксцесс стремится к отрицательной величине. Показатель эксцесса определяется по формуле:

Распределение оценивается как предположительно близкое к нормальному, если установлено, что от 50 до 80 % всех значений располагаются в пределах одного стандартного отклонения от среднего арифметического, и коэффициент эксцесса по абсолютной величине не превышает значения равного двум.
Распределение считается достоверно нормальным если абсолютная величина показателей асимметрии и эксцесса меньше их ошибок репрезентативности в 3 и более раз.
21. Биномиальное распределение.
Случайная величина В = X1 + X2 +…+ Xk называется биномиальной. Ясно, что 0 < B < k при всех возможных исходах опытов. Чтобы найти распределение В, т.е. вероятности Р(В = а) при а = 0, 1, …, k, достаточно знать р – вероятность наступления рассматриваемого события в каждом из опытов. Действительно, случайное событие В = а осуществляется тогда и только тогда, когда событие А наступает ровно при а испытаниях. Если известны номера всех этих испытаний (т.е. номера в последовательности испытаний), то вероятность одновременного осуществления в а опытах события А и в k-а опытах противоположного ему – это вероятность произведения k независимых событий. Вероятность произведения равна произведению вероятностей, т.е. ра( 1 - р)k-a. Сколькими способами можно задать номера а испытаний из k? Это  - число сочетаний из k элементов по а, рассматриваемое в комбинаторике. Как известно,
- число сочетаний из k элементов по а, рассматриваемое в комбинаторике. Как известно,
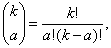
где символом k! обозначено произведение всех натуральных чисел от 1 до k, т.е.  (дополнительно принимают, что 0! = 1). Из сказанного следует, что биномиальное распределение, т.е. распределение биномиальной случайной величины, имеет вид
(дополнительно принимают, что 0! = 1). Из сказанного следует, что биномиальное распределение, т.е. распределение биномиальной случайной величины, имеет вид
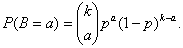
Название «биномиальное распределение» основано на том, что Р(В = а) является членом с номером (а +1) в разложении по биному Ньютона

если положить А = 1 – р, С = р. Тогда при j = a получим

Для числа сочетаний из k элементов по а, кроме  , используют более распространенное в отечественной литературе обозначение
, используют более распространенное в отечественной литературе обозначение  .
.
Для случайной величины В, имеющей биномиальное распределение, математическое ожидание и дисперсия выражаются формулами

22. Геометрическое распределение.
Пусть проводятся независимые испытания, каждое испытание может иметь два исхода: удача с вероятностью p и неудача с вероятностью q = 1 - p. Введем в рассмотрение случайную величину X — число испытаний до первого появления удачи. Эта случайная величина может принимать значения 1, 2, 3, 4 и так далее до бесконечности. Когда говорят, что случайная величина X имеет значение k, то это означает, что первые k - 1 испытание закончились неудачей, а k -ое испытание стало удачным. Вероятность того, что в серии независимых испытаний будет вначале k - 1 неудач, а в k -ое испытание — удача, равна  . Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность
. Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность  . Этот закон распределения и называется геометрическим распределением. Название происходит из того, что величина
. Этот закон распределения и называется геометрическим распределением. Название происходит из того, что величина  представляет собой геометрическую прогрессию, с первым членом p и знаменателем q. Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать:
представляет собой геометрическую прогрессию, с первым членом p и знаменателем q. Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать:  ,то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем:
,то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем:  .Для вычисления суммы воспользуемся следующим приемом — заменим
.Для вычисления суммы воспользуемся следующим приемом — заменим  на
на  и вынесем производную за знак суммы, в итоге получим:
и вынесем производную за знак суммы, в итоге получим:  .Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна
.Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна  . Вычисляя производную, запишем:
. Вычисляя производную, запишем:  .Аналогично можно получить выражение для
.Аналогично можно получить выражение для  :
:  .Заменяя сумму на ее значение
.Заменяя сумму на ее значение  , вычисляем:
, вычисляем:  .Таким образом, имеем выражение для дисперсии:
.Таким образом, имеем выражение для дисперсии:  .Если вероятность удачи равна единице, то математическое ожидание числа испытаний до первой удачи равно 1, а дисперсия — 0. Если, наоборот, вероятность удачи равна нулю, то математическое ожидание — бесконечность (то есть нужно произвести бесконечное число испытаний до появления удачи).
.Если вероятность удачи равна единице, то математическое ожидание числа испытаний до первой удачи равно 1, а дисперсия — 0. Если, наоборот, вероятность удачи равна нулю, то математическое ожидание — бесконечность (то есть нужно произвести бесконечное число испытаний до появления удачи).
23. Распределение Пуассона.
Если число испытаний n  и p 0 так, что np , > 0, то
и p 0 так, что np , > 0, то 
при любых k = 0, 1, 2, ….
Это означает, что при больших n и малых p вместо вычислений по точной формуле


можно воспользоваться приближенной формулой
 .
.
На практике пуассоновским приближением пользуются при npq= np (1-p) < 9.
24. Гипергеометрическое распределение.
Пусть имеется N предметов, из них M — помеченных. Наудачу вытаскивают n предметов. Какова вероятность, что среди вытащенных n предметов будет m помеченных? Разумеется  . Для решения задачи посчитаем общее число элементарных исходов, каким можно вытащить n предметов из N, и число благоприятных исходов, то есть когда среди n вытащенных предметов окажется m помеченных. Согласно формулам комбинаторики (см. квант 7) общее число элементарных исходов есть
. Для решения задачи посчитаем общее число элементарных исходов, каким можно вытащить n предметов из N, и число благоприятных исходов, то есть когда среди n вытащенных предметов окажется m помеченных. Согласно формулам комбинаторики (см. квант 7) общее число элементарных исходов есть  . Составить комбинацию m помеченных предметов, когда всего их M, можно
. Составить комбинацию m помеченных предметов, когда всего их M, можно  способами. При этом на каждый способ составить комбинацию m помеченных предметов из M есть
способами. При этом на каждый способ составить комбинацию m помеченных предметов из M есть  способов взять оставшиеся n - m предметов из N - M не помеченных. Таким образом, число благоприятных элементарных исходов есть
способов взять оставшиеся n - m предметов из N - M не помеченных. Таким образом, число благоприятных элементарных исходов есть  . Согласно классическому определению вероятности получаем ответ к задаче:
. Согласно классическому определению вероятности получаем ответ к задаче:  .Если значения N, M и n заданы, то полученная вероятность, рассматриваемая как функция m, представляет собой закон распределения случайной величины — числа помеченных предметов m в выборке n. Этот закон распределения называется гипергеометрическим распределением
.Если значения N, M и n заданы, то полученная вероятность, рассматриваемая как функция m, представляет собой закон распределения случайной величины — числа помеченных предметов m в выборке n. Этот закон распределения называется гипергеометрическим распределением
25. Равномерное распределение.
Пусть производится n независимых испытаний. Случайная дискретная величина X имеет равномерное распределение, если она принимает значения х i
(i= 1, n) с одинаковыми вероятностями
| p(x i)= | ||
| n |
Случайная непрерывная величина X на промежутке (а,b) имеет равномерное распределение, если плотность распределение
| p(x)= | ||
| b-a |
на заданном промежутке, а вне его р(х)=0.
Функция распределения в этом случае имеет вид:

Математическое ожидание и дисперсия случайной непрерывной величины X вычисляется следующим образом:
| M(X)= | a+b | |
| D(X)= | (b-a)2 | |
26. Показательное распределение.
Не нашли, что искали? Воспользуйтесь поиском: