Расст от тчки до прямой

Пусть прямая Lзадана ур-ем и дана точка , лежащая вне этой прямой, тогда расстояние d от тчки, М₀ до прямой L находится Если ур-е прямой L в виде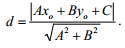

Вопрос №26

Вопрос 26. Окружностью называется геометрическое место точек, равноудаленных от точки, называемой центром окружности х₂ и у₂-координаты центра

Вопрос №27

27. Эллипс-это геометрическая фигура, которая ограничена кривой, заданной уравнением Фокусное расстояние и полуоси связаны соотношением: а2=в2+с2 Свойства: 1.Эллипс пересекает каждую из осей координат в двух точках.2.Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.3.Эллипс имеет две взаимно перпендикулярные оси симметрии

4.Эллипс имеет центр симметрии.

5.Эллипс может быть получен сжатием окружности.

Вопрос№28

Гипербола, ее характеристики, геометрические свойства Г.—это геометр место тчек плоскости, для кот-ых модуль разности расстояний от 2х заданн точек есть величина постоянн(и равна 2а). , каноническое ур-е гиперболы где b ² =a ² +c ². а наз-ют действит-ой полуосью гиперболы, число b - мнимой полуосью. гипербола симметр относ-но осей координат и, след-но, относ-но начала координат. Т.к. из канонич ур-я гиперболы следует, что то нет точек кривой в полосе -a > x > a.при ветви гиперболы неогран-но приближ-ся к прямым , не пересекая их.Число , кол-но характер-ее сжатие ветвей наз-ют эксцентриситетом гиперболы. Точки перес-я гиперболы с действ-ой осью наз-я вершинами гиперболы.2 прямые 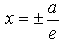наз-ют директрисами.

Вопрос №29.

Параболой наз.геометрическое место точек плоскости,для к-х расстояние от заданной точки (F) до заданной прямой директрисы есть величина постоянная.Исходя из определения расстояние от точки M до директрисы MK=MF,где MF=(x-p/2)²+y²=MK=x+p/2x²-px+p²/4+y²-x²-px-p²/4=0y²=2px -Каноническое уравнение параболы,ориентированной вдоль Оx,где p>0аналагично получено x²=2py вдоль ОyF (p/2;0)-в первом случае x=-p/2;F(0;p/2)-во 2-ом случае y=-p/2;Для эллипса эксцентриситет 0<E<1Для гиперболы E>1Для параболы E=1;

Вопрос №30.

Общее уравнение плоскости имеет вид, где коэффициенты A,B,C одновременно не равны нулю.угол между плоскостями находится по формуле: На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей. Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если: =0Плоскости параллельны, векторы нормалей коллинеарны: ïï .Это условие выполняется, если:

Вопрос№31

Не нашли, что искали? Воспользуйтесь поиском: