Понятие окрестности точки. Предельная, изолированная, внутренняя, внешняя точки множества. Открытые и закрытые множества.

Окрестность тчки -множ-во,содеж-ее данную точку, и близкие к ней. 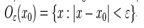Внутренняя точка множ-ва-тчка, входящая в это множ-во вместе со своей окрестностью. Открытое множ-во – это множ-во, каждый эл-т которого входит в него вместе со своей окрестностью.

Вопрос №36

Придел числовой последовательности. Сходящиеся и расходящиеся последовательности. Бескон-но большие и бескон-но малые(б.м.) послед-сти; связь межу ними. Св-ва бесконечно малых и сходящихся последовательностей (сход. послед.). Предел последовательности(1+ )ⁿ, при n Если каждому натуральному числу n поставлено в соответствии число x_n, , то говорят, что задана числовая последовательность (последовательность чисел) или просто последовательность x₁,x₂,…x_n.Последовательность, которая имеет предел, называется сходящейся; иначе - расходящейся. Последовательность a_nназыв. бесконечно большой, если предел lim а_n(n-> 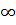)= 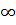,бесконечно малой lim а_n(n-> 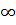)=0.Св-ва бесконечно малых:1.Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность2.Произведение любого конечного числа б. м. последовательность есть б.м. последовательность3.Произведение ограниченной последоват. на б. м. есть последовательность б.м.Св-ва сход. послед.:1.Имеет единственный предел2.Всякая послед. сходящейся послед. сходится у тому же пределу.3.Сход. послед. Ограничена.4. 3. Если последовательность монотонна и ограниченна, то она сходится.5. если a_nb_nсход. послед.Причем limа_n(n-> 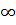)=a, lim а_n(n-> 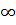)=b, тоlimа_n + b_n=a , lim а_n * b_n(n-> 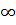)=a 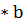, lim c* c_n(n-> 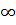)=c*a(c=const)Рассмотрим последовательность (1+ )ⁿ, при n . Доказывается, что эта последовательность монотонная огранич. и возрастающая => имеет придел и этот придел обознач. е=2,718(Эйлерово число) т.е. 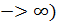предел (1+ )ⁿ(n =е

Вопрос№37

Понятие функции. Способы задания функции, операций над ними. Обратная функция. Элементарные функции, их классификация. Функцией называется закон, по которому числу х 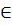Х, поставлено в соответствие только одно число у, пишут 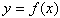, при этом x называют аргументом функции, y называют значением функции. способы задания функций: 1. АналитическийЗаключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например .2. ТабличныйТабличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Пример:

3.ГрафическийПри графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом .Функцию называют обратной функцией по отношению к функции y=f(x). Функция y=f(x) и y= f^-1(x) называют взаимообратными. Элементарные функции 1.степенные у 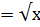y=x^-1 и т.д.

2. показательные y = a^x 3.логарифмические y = log _ax 4. тригонометрические y = sin xy = cos x и т.д. 5. обратные тригонометрические. y = arcsin xy = arccos x и т.д.

Вопрос№38

Предел функции на бесконечности и в точке. Односторонние приделы.

Число А назыв. пределом функции y=f(x) при x 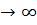, если для любого сколь угодно малого положительного числа 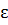найдется такое число S>0, что для всех x таких что модуль x>S выполн. Неравенство модуль F(x)-A<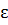

A=lim_x->x0f(x)ó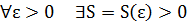

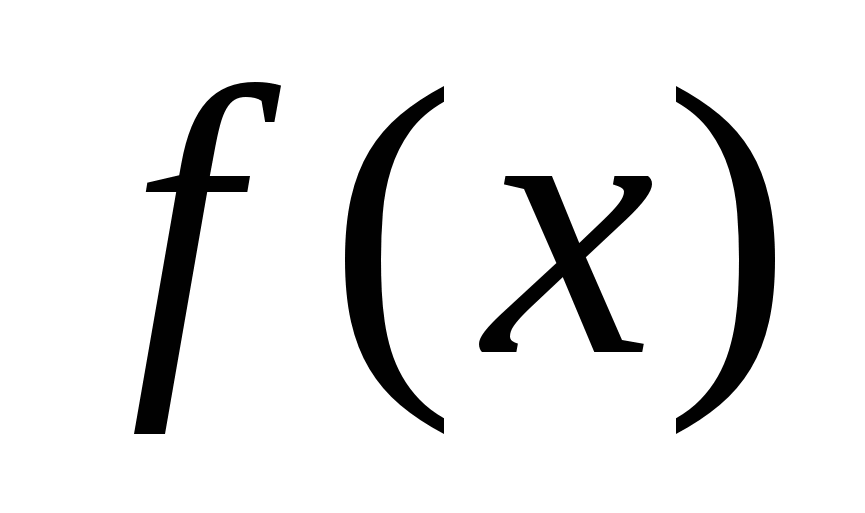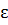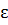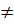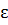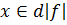Число А называется пределом функции в точке x х₀(или или в точке x₀₎, если для любой сколь угодно малого полож. числа найдется такое полож. число зависящее от , что для всех x x и таких, что /x-x₀/< выполняется неравенство /f(x)-A/< .Различают правый односторонний придел и левый односторонний придел:Число называется правым односторонним пределом функции в точке , если для такое, что для любого и 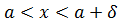, выполняется неравенство 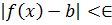. 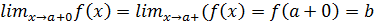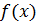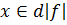Правый предел обозначается Число называется левым односторонним пределом функции в точке , если для такое, что для любого и 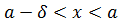и, выполняется неравенство 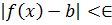. Левый предел обозначается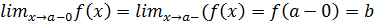

Вопрос№39

Не нашли, что искали? Воспользуйтесь поиском: