
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Язык логики высказываний. Определение формулы логики высказываний.
Поскольку логика изучает формы мышления, а мышление неразрывно связано с языком, постольку логика является также наукой о языке.
Язык - это любая знаковая информационная система (система слов или знаков), выполняющая функцию формирования, хранения и передачи информации в процессе познания действительности и общения между людьми.
По происхождению языки бывают естественные и искусственные.
Естественные языки - исторически сложившиеся в обществе звуковые и графические знаковые системы. Естественные языки возникают стихийно в процессе совместной деятельности и общения людей и народов. К естественным относятся языки разных народов, язык жестов и т. п.
Искусственные языки - вспомогательные знаковые системы, создаваемые группами людей специально - для более точной передачи специфической информации. К искусственным языкам относятся нотные знаки, знаки кодовых систем, шифры, азбука Морзе, «блатной язык», которым пользуются преступники, и т. п.
Существуют также смешанные языки, базой в которых выступает естественный (национальный) язык, дополняемый символикой и условными обозначениями, относящимися к конкретной предметной области. К этой группе языков относится язык формальной логики.
В качестве символов выступают определенные знаки. Знак- любой чувственно воспринимаемый предмет, который заменяет, представляет другой предмет, используемый в процессе познания или общения в качестве представителя какого-либо объекта.
В логике различают языки логики высказываний и логики предикатов. Язык логики высказываний используется для описания структуры высказываний, рассуждений, предложений. Под высказываниями понимаются простые или сложные абстрактные символические выражения, обозначающие суждения. Простые высказывания, объединенные в сложные с помощью связок «и», «или», «если.., то» и др., называют пропозициональными высказываниями, а логику, с помощью которой описываются такие высказывания, иногда называют пропозициональной логикой, или пропозициональным исчислением. Логика высказываний может быть классической (двузначной) или многозначной.
Язык логики предикатов используется для описания внутренней структуры высказываний. Алфавит языка логики предикатов состоит из следующих символов:
а) а, Ь, с... - постоянные предметные термины;
б) x,y,z...- переменные предметные термины;
в) Р, Q, R... - предикатные термины (имена свойств);
г) p, q, r... - пропозициональные термины (имена высказываний);
д) кванторы: - все, - некоторые;
е),,, - логические союзы, которые соответственно читаются: «и», «или», «если…,то...», «если, и только если, то...» и называются знаком отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности;
ж) технические знаки:, - запятая; () - скобки.
С помощью приведенного алфавита строится формализованная логическая система, называемая исчислением предикатов. Выражения языка логики предикатов называются формулами. Формулы могут быть правильно построенные и неправильно построенные.
Существует особая наука о знаках - семиотика. В этой науке выделяют три раздела - синтаксис, семантику и прагматику, что связано с наличием трех аспектов языка.
Синтаксисом называется раздел семиотики, в котором исследуются отношения между самими знаками (правила построения и преобразования выражений языка и т. д.). В процессе этого исследования отвлекаются от смыслов и значений знаков.
Семантикой называется раздел семиотики, в котором прежде всего исследуются отношения знаков к представляемым ими объектам, а также смыслы знаков, поскольку они являются одним из средств установления связи знаков и их значений.
Базовая семантическая таблица для сложных формул:
| А | В | А˄В | А˅В | А→В | А_˅_В | А≡В | ┐А | ┐В |
| И | И | И | И | И | Л | И | Л | И |
| И | Л | Л | И | Л | И | Л | Л | И |
| Л | И | Л | И | И | И | Л | И | Л |
| Л | Л | Л | Л | И | Л | И | И | И |
Прагматика изучает отношение человека к знакам, а также отношения между людьми в процессе знакового общения.
Язык формальной логики позволяет избегать неясности и двусмысленности естественного языка и сводить процесс проверки правильности рассуждений к «вычислению».
В ряде случаев в процессе логического анализа для выяснения некоторых логических отношений (логического следования, совместимости, несовместимости высказываний и др.) не играют роли структуры простых высказываний. Не учитывать такие структуры (если в этом действительно нет необходимости) позволяет так называемый язык классической логики высказываний, использующий пропозициональные переменные.
Формулы (индуктивное определение):
1) каждая пропозициональная переменная есть формула;
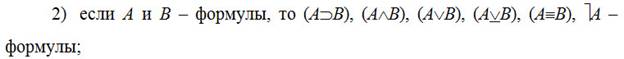
3) ничто, кроме указанного в пунктах 1 – 2, не есть формула.

Пример. «Вы получите положительную оценку по логике тогда и только тогда, когда вы решите все предлагаемые вам задачи и не будете шуметь на лекциях». Обозначим простые высказывания при помощи пропозициональных переменных: p – «Вы получите положительную оценку по логике»; q – «Вы решите все предлагаемые вам задачи»; r – «Вы будете шуметь на лекциях». Тогда получится формула:
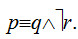
Не нашли, что искали? Воспользуйтесь поиском: