
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Общая характеристика понятий. Омский государственный университет
Омский государственный университет
Н. А. Черняк
Логика
Учебное пособие для студентов I – II курсов
Издание ОмГУ
Омск 2004
УДК 161
ББК 87.4 я 73
Ч-498
Рецензенты: д.филос.н., проф. В.И. Разумов
к.филос.н., доц. Л.М. Карпова
Черняк Н.А.
Логика: Учебное пособие. Омск: Омск. Гос. ун-т, 2004. – 61 с.
В пособии в краткой форме излагается основное содержание курса логики, разработанного в соответствии с программой для высших учебных заведений. Рекомендуется студентам I-II курсов.
© Н.А. Черняк, 2004
© Омский госуниверситет, 2004
Предмет логики
Формальная логика – наука о законах и формах мышления. Термин «логика» имеет свое происхождение от греческого logos, что означает «мысль», «слово», «разум», «закон».
Логика исследует логические формы, отвлекаясь от их конкретного содержания, анализирует мышление со стороны его формальной правильности.
Формальная правильность означает соответствие мышления (рассуждения, доказательства) известным фиксированным правилам, соблюдение которых обеспечивает правильность перехода от одних высказываний к другим.
Предметом логики является выводное знание, то есть знание, полученное из ранее проверенных истин в соответствии с определенными законами. Логику не интересует в каждом отдельном случае истинная характеристика исходного знания. Ее задача заключается в том, чтобы определить, следует ли вывод из определенных посылок с необходимостью либо лишь вероятно.
Другой задачей, вытекающей из уже указанной, является формализация и систематизация правильных способов рассуждений.
Формальная логика сегодня представлена двумя науками – традиционной и математической (символической) логикой.
Традиционная логика – это первая ступень логики выводного знания. Она изучает общечеловеческие формы мысли (понятия, суждения), формы связи мыслей в рассуждении (умозаключения), зафиксированные в системе формально-логических законов (тождества, противоречия, исключенного третьего и достаточного основания).
Основоположником традиционной логики считается Аристотель (384-322 гг. до н. э.). Ему принадлежит заслуга разработки основных логических категорий и законов, а также систематического и последовательного изложения логического учения.
Изучение форм мышления и символическое обозначение их элементов, начатое ещё Аристотелем в IV в. до н. э., было продолжено затем Г. В. Лейбницем, Дж. Локком, Дж. Булем, П. Порецким, Г. Фреге, Б. Расселом, Д. Гильбертом, А. Тарским, Я. Лукасевичем и другими математиками и логиками. Это открыло перспективный путь исследования материальных объектов, когда, отвлекаясь от внутренней изменчивости этих объектов и их вещественного субстрата, содержание изучаемого явления выражают с помощью фиксированных элементов его формы. Данное обстоятельство позволило заменить вывод какого-либо содержательного предложения выводом формулы, её выражающей. Мышление стало исследоваться с помощью формализованных языков (логических исчислений), а формализованные языки послужили основой для разработки языков, которыми пользуются в вычислительных машинах.
Математическая логика – вторая после традиционной логики ступень в развитии формальной логики, применяющая математические методы и специальный аппарат символов и исследующая мышление с помощью исчислений (формализованных языков). Большая, чем в традиционной логике, степень абстрагирования и обобщения позволяет современной символической логике познавать новые закономерности мышления, возникающие при решении сложных логических конструкций в математике, кибернетике, при проектировании и в работе электронно-вычислительных машин и управляющих устройств.
С помощью логического аппарата и найденных законов логического следования математическая логика дала возможность по- новому осмыслить законы и правила традиционной логики и решить такие проблемы, которые долгое время оставались нерешёнными. Это относится, прежде всего, к теории вывода, т. е. к самому существенному в предмете формальной логики.
Значение логики заключается в том, что она учит, как правильно по форме построить рассуждение, чтобы, при условии верного применения формально-логических законов, из истинных посылок прийти к истинному выводу, расширяющему наши знания.
Понятие логической формы. Логическая форма – это структура мысли или способ связи элементов ее содержания. Логическая форма выражается посредством логических переменных и логических констант. В качестве логической переменной может выступать любая буква латинского алфавита: A, B, C, p, q. Константы или логические постоянные выступают способом связи логических переменных и выражаются словами «все», «некоторые», «суть», «и», «или», «либо, либо», «если…, то» и т.д. Для обозначения логических констант употребляются символы. Этим достигается большая компактность и строгость изложения. Примерами логических констант являются:
" (x) – квантор общности «для всякого x верно, что».
$ (x) – квантор существования – «существуют x».
Ù - логический союз конъюнкция, выражается посредством грамматических союзов «и», «да», «но».
Ú - логический союз дизъюнкция в значении грамматического союза «или…или».
® - логический союз импликация, выражается словами «если, то».
Пропозициональная функция – это выражение, содержащее переменные и превращающееся в высказывание при подстановке вместо этих переменных соответствующих дескриптивных терминов.
Законы мышления
Закон мышления или логический закон – это суждение, выражающее внутреннюю необходимую существенную связь между мыслями либо их элементами в процессе рассуждения или доказательства.
В формальной логике выделяют четыре основных закона: тождества, противоречия, исключенного третьего и достаточного основания. Эти законы являются основными потому, что выражают наиболее общие свойства мышления: определенность, непротиворечивость, последовательность и обоснованность.
Законы формальной логики – это законы построения и связи мыслей. Они отражают схемы правильных рассуждений, сложившиеся в процессе многовековой практики мышления. Эти законы лежат в основе различных логических операций, умозаключений, доказательств, носят объективный характер, т.е. не зависят от сознания и воли людей.
Хотя законы логики являются законами мышления, но не самих вещей, они имеют глубокую объективную основу – относительную устойчивость, качественную определенность, взаимообусловленность предметов материального мира.
Закон тождества фиксирует одно из коренных свойств мышления – его определенность. Согласно этому закону всякая мысль в процессе рассуждения должна быть тождественна самой себе. Это означает, что предмет мысли должен рассматриваться в одном и том же содержании своих признаков на всем протяжении рассуждения или доказательства.
Из существа этого закона вытекает важное требование: нельзя нетождественные мысли принимать за тождественные, нельзя различные мысли принимать за тождественные. Мысль должна быть сформулирована таким образом, чтобы не допускалась многозначность используемых терминов.
В математической логике этот закон выражается в виде тождественно-истинных формул:
p ® p – если р, то р
р «р – р эквивалентно (равнозначно) р
"х (р(х) ® р(х)) – для всякого предмета х верно, что если х имеет р, то х имеет это свойство.
Нарушение требования, вытекающего из закона тождества, ведет к логической ошибке – «подмене понятия». Сущность ее состоит в том, что вместо данного понятия употребляется другое.
Отождествление понятий чаще всего происходит неосознанно, в силу многозначности языка, однако иногда подмена производится преднамеренно, сознательно.
Закон противоречия выражает требование непротиворечивости и последовательности мышления. Это значит, что признав известные положения в качестве истинных и развивая выводы из этих положений, мы не можем допустить в своем рассуждении или доказательстве никаких утверждений, противоречащих тому, что было сказано ранее.
Закон противоречия гласит: два находящихся в отношении отрицания суждения не могут быть одновременно истинными; по крайней мере одно из них необходимо ложно. Следует иметь в виду, что данный закон действителен лишь в отношении тех суждений, в которых говорится об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении. В случаях, где данное условие не выполняется, закон противоречия неприменим.
Закон противоречия имеет силу как в отношении контрарных (противоположных), так и контрадикторных (противоречащих) высказываний.
В математической логике закон противоречия выражается формулой:
 – неверно, что могут быть одновременно истинными суждения
– неверно, что могут быть одновременно истинными суждения  и его отрицания
и его отрицания 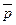 .
.
Закон исключенного третьего. Согласно этому закону, из двух противоречащих высказываний одно и только одно истинно. Это тот случай, когда «третьего не дано», т.е. истинное высказывание не может заключаться между противоречащими высказываниями.
Противоречащими называются суждения, в одном из которых что-либо утверждается (или отрицается) о каждом предмете некоторого множества, а в другом отрицается (утверждается) о некоторой части этого множества. Эти суждения не могут быть одновременно ни истинными, ни ложными: если одно из них истинно, то другое непременно ложно и наоборот.
Подобно закону противоречия закон исключенного третьего выражает последовательность и непротиворечивость мышления. Он требует ясных определенных ответов, указывая на невозможность отвечать на один и тот же вопрос в одном и том же смысле и «да» и «нет», на невозможность искать нечто среднее между утверждением чего-либо и отрицанием того же самого.
В математической логике этот закон имеет формулу  – р или неверно, что р.
– р или неверно, что р.
Закон достаточного основания выражает требование доказательности, обоснованности мысли. Согласно этому закону, всякая истинная мысль должна быть обоснована другими мыслями, истинность которых уже доказана. Мысли (суждения), которые приводятся для обоснования истинности других мыслей, называются логическим основанием. Мысль, которая вытекает из других как из основания, называется логическим следствием.
Логическую связь между основанием и следствием необходимо отличать от причинно-следственной связи. Причинно-следственная связь является выражением объективных отношений между предметами материального мира. Логическое отношение основания и следствия выражает связь между высказываниями, не всегда причинно-следственная связь совпадает с логической.
Закон достаточного основания имеет важное теоретическое и практическое значение.
Фиксируя внимание на требовании указания аргументов (оснований), обладающих достаточной силой доказательности, этот закон помогает отделить истину от ложности, тем самым прийти к верным выводам. Чрезвычайно большое значение закон достаточного основания имеет в юридической практике.
Формально-логические законы - это законы нормативного мышления. Соблюдение требований законов логики предохраняет мышление от логических ошибок и гарантирует получение истинного знания при условии, если исходное знание будет истинным.
Вопросы для повторения
1. Что такое логика и какое значение она имеет для других наук?
2. Что такое логическая форма и логический закон?
3. Каково соотношение между формальной правильностью и истинностью мысли?
4. Какие основные требования мышления выражают законы логики?
Понятие
Общая характеристика понятий
Понятие – это форма мысли, посредством которой предметы выделяются и обобщаются по существенным признакам. Понять нечто, т.е. составить понятие о предмете, это значит выразить сущность этого предмета. Этим понятие отличается от других познавательных форм – ощущения, восприятия, представления, которые не обладают такой обобщающей и абстрагирующей силой и, следовательно, в своем содержании не могут выразить закономерностей.
Как логическая форма понятие характеризуется двумя важнейшими параметрами – содержанием и объемом.
Содержание понятия - это совокупность существенных признаков предметов, на основании которых они выделяются и обобщаются.
Объем понятия - это предмет или совокупность предметов, обладающих признаками, составляющими содержание понятия.
Совокупность предметов, охватываемая объемом понятия, называется логическим классом, или множеством, а отдельный предмет объема понятия – элементом класса (множества).
Класс (множество) может включать в себя подклассы, или подмножества. Например, класс городов включает в себя подкласс городов России, класс рек – подкласс рек Сибири и т.д.
Понятие, из объема которого происходит выделение подкласса, называется родовым или родом; понятие, объем которого выделяется из родового понятия – видовым или видом (например, «наука» – родовое понятие, «юриспруденция» – видовое).
Содержание и объем понятия тесно связаны друг с другом. Эта связь выражается в законе обратного отношения между объемом и содержанием, согласно которому увеличение содержания понятия ведет к уменьшению его объема и наоборот. Или иначе: если объем одного понятия включает в себя объем другого понятия, то содержание первого понятия является частью содержания второго.
Не нашли, что искали? Воспользуйтесь поиском: