
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Законы сложения и умножения
1. Закон идемпотентности (подобия) – класс, сложенный сам с собою, или умноженный на себя, равен самому себе.
A 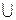 A=A
A=A
А ∩ А=А
2. Закон коммутативности – результат сложения и умножения не зависит от того, в каком порядке берутся эти классы.
A 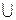 В= В
В= В 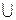 A
A
А ∩ В= В ∩ А
3. Закон ассоциативности – результат сложения и умножения более чем двух классов не зависит от порядка выполнения действий.
A 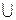 (В
(В 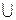 С)= (А
С)= (А 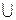 В)
В) 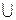 С
С
А ∩ (В ∩ С)= (А ∩ В) ∩ С.
4а. Закон элиминации (поглощения) для сложения относительно умножения – сумма какого-либо класса и произведения двух классов, одним из сомножителей которого является этот класс, равна этому классу.
A 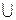 (А ∩ В) = А
(А ∩ В) = А
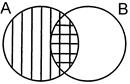
= А
4б. Закон элиминации для умножения относительно сложения – произведение какого-либо класса и суммы двух других классов, одним из слагаемых которой является этот класс, равно умножаемому классу.
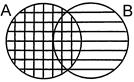 А ∩ (А
А ∩ (А 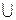 В) = А.
В) = А.
= А
5а. Закон дистрибутивности умножения относительно сложения.
А ∩ (В 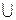 С) = (А ∩ В)
С) = (А ∩ В) 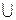 (А ∩ С).
(А ∩ С).

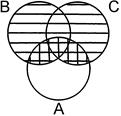
=
5б. Закон дистрибутивности сложения относительно умножения
A 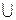 (B ∩ C) = (A
(B ∩ C) = (A 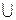 B) ∩ (A
B) ∩ (A  C)
C)
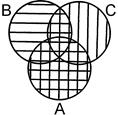

=
Законы дополнения
Законы дополнения вытекают из свойств противоречащих понятий, каковыми являются дополнение и дополняемое понятие.
1.
 |
Сумма класса и его дополнения равна универсальному классу А
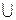 A' = 1.
A' = 1.
2. Сумма дополняемого класса и универсума равна универсальному классу
А  1=1.
1=1.
3.
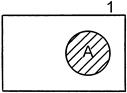 |
Произведение дополняемого класса и универсума равно дополняемому классу А ∩ 1 = А.
4. Произведение класса и его дополнение является пустым классом
А ∩ A' = 0.
5. Дополнением универсума является пустой класс 1' = 0.
6. Дополнением дополнения является дополняемый класс (A') ' = A.
Не нашли, что искали? Воспользуйтесь поиском: