
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Правила выводов логики высказываний
Логика высказываний – это логическая система, которая анализирует процессы рассуждения, опираясь на истинностные характеристики логических связок и отвлекаясь от внутренней структуры суждений.
Логика высказываний может строиться табличным методом или как исчисление, т.е. как система, позволяющая получать одни выражения из других на основании известных правил. Последняя называется системой натурального вывода. Аппаратом в ней служат правила вывода, каждое из которого является элементарной формой умозаключения.
Правила вывода – это предписания или разрешения, позволяющие из суждений одной логической структуры как посылок вывести суждение некоторой логической структуры как заключение. Их особенность заключается в том, что признание истинности заключения производится на основании не содержания посылок, а их структуры.
Правила вывода записываются в виде схемы, которая состоит из двух частей (верхней и нижней), разделенных горизонтальной линией – над чертой выписываются логические схемы посылок, под ней – заключение.
Схема правил вывода:

Читается: из посылок вида  можно вывести заключение В.
можно вывести заключение В.
Правила выводов логики высказываний делят на основные и производные.
Основные правила – более простые и очевидные.
Производные выводятся из основных. Их введение сокращает процесс вывода.
Как основные, так и производные делятся на прямые и непрямые (косвенные).
Прямые правила указывают на непосредственную выводимость некоторых суждений из других суждений.
Непрямые (косвенные) правила выводов дают возможность заключить о правомерности некоторых выводов из правомерности других выводов.
Основные прямые правила:
Правила введения и удаления конъюнкции (В.К.), (У.К.):
В.К.

У.К.


Правила введения и удаления дизъюнкции (В.Д.), (У.Д.):
В.Д.

У.Д.
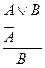

Правила удаления импликации (У.И.):

Правила введения и удаления эквивалентности (В.Э.), (У.Э.):
В.Э.
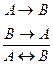
У.Э.
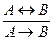


Правила введения и удаления двойного отрицания (В.О.), (У.О.):
В.О. 
У.О. 
Не нашли, что искали? Воспользуйтесь поиском: