Контрольная работа №1 4 страница

z = 3xy + 4y² – 6x; A (4; 5); B (4,04; 4,95).

Задание 10.

Дана функция z = f (x; y), точка А (x₀; y₀) и вектор (а₁; а₂). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .

z = ^; A (3; 4); a (-3; 4).

Задание 11.

Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.

а) б) ; в) г)

Задание 12.

Вычислить приближенное значение определенного интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 13.

Вычислить несобственный интеграл или доказать его расходимость.

Задание 14.

Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной полуэллипсом 2у = 3 и параболой 4у = 4 – х².

Задание 15.

Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).

(х² + у²)⁵ = а⁶ ху³.

Задание 16.

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.

х = 0, у = 0, z = 0, x + у = 1, z = x² + 3y².

Задание 17.

Вычислить криволинейный интеграл

где С есть окружность x = R cos t, y = R sin t, пробегаемая по ходу часовой стрелки.

Вариант 16

Задание 1.

Найти производные данных функций.

а)

б)

в)

г) ;

д)

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а) у = ln (2x-3); б) x (t) = 3(t – sin t); y = 3(1 – cos t).

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,61, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f (x) =

Задание 5.

Найти наибольший объем цилиндра, у которого полная поверхность равна S.

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б)

Задание 7.

Составить уравнения касательной и нормальной плоскости к винтовой линии в точке

Задание 8.

Дана функция z = f (x; y). Показать, что:

F .

z = F =

Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, поучающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = 2x² + 2y² + 10x + 8y; A (6; 4); B (6,05; 3,98).

Задание 10.

Дана функция z = f (x; y), точка А (x₀; y₀) и вектор (а₁; а₂). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .

z = ; A (1; -2); a (1; 2).

Задание 11.

Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.

а) б) ; в) г)

Задание 12.

Вычислить приближенное значение определенного интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 13.

Вычислить несобственный интеграл или доказать его расходимость.

Задание 14.

Вычислить длину дуги полукубической параболы у = х^3/2 от х = 0 до х = 5.

Задание 15.

Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).

(х² + у²)⁵ = а⁴ х⁴ у².

Задание 16.

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.

х = 0, у = 0, z = 0, x = 1, х + у = 2, z = x² + y².

Задание 17.

Вычислить криволинейный интеграл

по любому пути, соединяющему точки (0; 0) и (3; 4).

Вариант 17

Задание 1.

Найти производные данных функций.

а)

б)

в)

г) ;

д) .

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а) у = x sin x; б) x = t² – 2 t; y = .

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,29, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f (x) =

Задание 5.

Определить максимальную площадь равнобедренного треугольника, боковая сторона которого равна l.

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б)

Задание 7.

Составить уравнение касательной и нормальной плоскости к кривой в точке .

Задание 8.

Дана функция z = f (x; y). Показать, что:

F .

z = F =

Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, поучающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = x² - y² –3xy; A (-2; 3); B (-1,98; 2,97).

Задание 10.

Дана функция z = f (x; y), точка А (x₀; y₀) и вектор (а₁; а₂). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .

z = x²у +xy²; A (1; 1); a (6; -8).

Задание 11.

Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.

а) б) ; в) г)

Задание 12.

Вычислить приближенное значение определенного интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 13.

Вычислить несобственный интеграл или доказать его расходимость.

Задание 14.

Вычислить длину кривой 2у = е^х + е^-х от х = 0 до х = ln3.

Задание 15.

Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).

(х² + у²)³ = а⁴ у².

Задание 16.

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.

х = 0, у = 0, z = 0, у + z = 1, x = y² + 1.

Задание 17.

Вычислить криволинейный интеграл

где С есть окружность x = R cos t, y = R sin t, пробегаемая против хода часовой стрелки.

Вариант 18

Задание 1.

Найти производные данных функций.

а)

б)

в)

г)

д) .

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а) у = x ; б) x = e^2t; y = .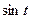

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,69, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f (x) =

Задание 5.

Определить наименьшую площадь равнобедренного треугольника описанного вокруг окружности радиуса r.

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б)

Задание 7.

Составить уравнения касательной и нормальной плоскости кривой в точке .

Задание 8.

Дана функция z = f (x; y). Показать, что:

F .

z = F =

Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, поучающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = 2x² + 4xy + 6y²; A (4; 2); B (3,96; 2,04).

Задание 10.

Дана функция z = f (x; y), точка А (x₀; y₀) и вектор (а₁; а₂). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .

z = ln (2x +3y); A (2; 2); a (-3; 2).

Задание 11.

Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.

а) б) ; в) г)

Задание 12.

Вычислить приближенное значение определенного интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 13.

Вычислить несобственный интеграл или доказать его расходимость.

Задание 14.

Вычислить длину дуги кривой

от t = 0 до t = .

Задание 15.

Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).

(х² + у²)³ = а⁴ х².

Задание 16.

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.

z = 0, z = , у = x².

Задание 17.

Вычислить криволинейный интеграл

по любому пути, соединяющему точки (1; 2) и (3; 6).

Вариант 19

Задание 1.

Найти производные данных функций.

а)

б)

в)

г) ;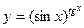

д) .

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а) у = ; б) x = sin t; y = t - 3t³.

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,51, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f (x) =

Задание 5.

Канал, ширина которого 27м. под прямым углом впадает в другой канал шириной 64 метра. Какова наибольшая длина бревен, которые можно сплавлять по этой системе каналов?

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б)

Задание 7.

Составить уравнения касательной и нормальной плоскости кривой в точке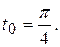

Задание 8.

Дана функция z = f (x; y). Показать, что:

F .

z =

F =

Задание 9.

Дана функция Z = F (x; y) и две точки А (x₀; y₀) и В (x₁; y₁). Требуется: 1) вычислить значение z₁ в точке В; 2) вычислить приближенное значение `z₁ функции в точке В, исходя из значения z₀ функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, поучающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x₀; y₀; z₀).

z = 4xy + 6y² – 10x; A (2; 4); B (1,97; 4,03).

Задание 10.

Дана функция z = f (x; y), точка А (x₀; y₀) и вектор (а₁; а₂). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора .

z = arctg ; A (-1; 1); a (1; -1).

Задание 11.

Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.

а) б) ; в) г)

Задание 12.

Вычислить приближенное значение определенного интеграла с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 13.

Вычислить несобственный интеграл или доказать его расходимость.

Задание 14.

Найти длину дуги гиперболической спирали = 1 от точки А (2;1/2) до точки В (1/2; 2).

Задание 15.

Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).

(х² + у²)³ = а²(2х² + у²).

Задание 16.

Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.

х = 0, у = 0, z = 0, z = y², у + x = 2.

Задание 17.

Вычислить криволинейный интеграл

вдоль параболы от точки А (0; 0) до точки В (1; 2).

Вариант 20

Задание 1.

Найти производные данных функций.

а) ;

б)

в)

г) ;

д) .

Задание 2.

Найти и для заданных функций: а) у = f (x); б) x = (t), у = (t).

а) у = 1/4x² (2ln x – 3); б) x = cos² t; y = 3 sin t.

Задание 3.

Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = e^x, вычислить значение e^a при а = 0,81, с точностью до 0,001.

Задание 4.

Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].

f (x) =

Задание 5.

По двум улицам движутся к перекрестку две автомашины с постоянными скоростями u₁ и u₂ . Считая, что улицы пересекаются под прямым углом, и зная, что в некоторый момент времени автомашины находятся от перекрестка на расстояниях a₁ и а₂ , определить, через какое время расстояние между ними станет наименьшим.

Задание 6.

Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.

а) б)

Не нашли, что искали? Воспользуйтесь поиском: