
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Контрольная работа №1 2 страница
х4 = а2 (3х2- у2).
Задание 16.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, у + z = 4, x2 + у2 = 4.
Задание 17.
Вычислить криволинейный интеграл

вдоль верхней половины 1 эллипса х = 3 cos t, у = 2 sin t, ( ).
).
Вариант 6
Задание 1.
Найти производные  данных функций.
данных функций.
а) 
|
б) 
|
в) 
|
г) 
|
д) 
|
Задание 2.
Найти  и
и  для заданных функций: а) у = f (x); б) x =
для заданных функций: а) у = f (x); б) x =  (t), у =
(t), у =  (t).
(t).
а) у = ectg3x; б) x = 3 cos t; y = 4 sin2 t.
Задание 3.
Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = ex, вычислить значение ea при a=0,55, с точностью до 0,001.
Задание 4.
Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f (x) =  .
.
Задание 5.
При каких линейных размерах закрытая цилиндрическая банка данной вместимости, будет иметь наименьшую полную поверхность?
Задание 6.
Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.
а)  б)
б)  .
.
Задание 7.
Найти уравнения касательной, уравнение нормальной плоскости линии r = r (t) в точке t0.

Задание 8.
Дана функция z = f (x; y). Показать, что:
F  .
.
z = 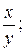 F =
F = 
Задание 9.
Дана функция Z = F (x; y) и две точки А (x0; y0) и В (x1; y1). Требуется: 1) вычислить значение z1 в точке В; 2) вычислить приближенное значение `z1 функции в точке В, исходя из значения z0 функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, поучающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x0; y0; z0).
z = x2 + y2 + 2x + y – 1; A (2; 4); B (1,98; 3,91).
Задание 10.
Дана функция z = f (x; y), точка А (x0; y0) и вектор  (а1; а2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора
(а1; а2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора  .
.
z = arctg (xy2); A (2; 3); a (4; -3).
Задание 11.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а)  б)
б)  ; в)
; в) 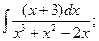 г)
г) 
Задание 12.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 13.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 14.
Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченном полуэллипсом у = 3  , параболой х =
, параболой х =  и осью Оу.
и осью Оу.
Задание 15.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
х6 = а2 (х4- у4).
Задание 16.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, 4z = у2, 2x - у = 0, х + у = 9.
Задание 17.
Вычислить криволинейный интеграл

вдоль ломанной t = ABC, где А (1; 2); В (1; 5); С (3; 5). Сделать чертеж.
Вариант 7
Задание 1.
Найти производные  данных функций.
данных функций.
а) 
|
б) 
|
в) 
|
г)  ; ;
|
д)  . .
|
Задание 2.
Найти  и
и  для заданных функций: а) у = f (x); б) x =
для заданных функций: а) у = f (x); б) x =  (t), у =
(t), у =  (t).
(t).
а) у = ex cos x; б) x = 3 t – t3; y = 3 t3.
Задание 3.
Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = ex, вычислить значение ea при а = 0,37, с точностью до 0,001.
Задание 4.
Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f (x) =  .
.
Задание 5.
Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен а. При каких размерах сторон прямоугольника окно будет пропускать наибольшее количество света?
Задание 6.
Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.
а)  б)
б)  .
.
Задание 7.
Найти уравнения касательной, уравнение нормальной плоскости линии r = r (t) в точке t0.

Задание 8.
Дана функция z = f (x; y). Показать, что:
F  .
.
z =  F =
F = 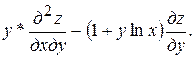
Задание 9.
Дана функция Z = F (x; y) и две точки А (x0; y0) и В (x1; y1). Требуется: 1) вычислить значение z1 в точке В; 2) вычислить приближенное значение `z1 функции в точке В, исходя из значения z0 функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, поучающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x0; y0; z0).
z = 3x2 + 2y2 + xy; A (-1; 3); B (-0,98; 2,97).
Задание 10.
Дана функция z = f (x; y), точка А (x0; y0) и вектор  (а1; а2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора
(а1; а2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора  .
.
z = arсsin (x2 / y); A (1; 2); a (5; -12).
Задание 11.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а)  б)
б) 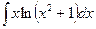 ; в)
; в)  г)
г) 
Задание 12.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 13.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 14.
Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми у = 2 / (1+x2) и у = x2.
Задание 15.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
х4 = а2 (х2 - 3 у2).
Задание 16.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, х2 + у2 = z, x2 + у2 = 4.
Задание 17.
Вычислить криволинейный интеграл

вдоль дуги 1 кривой у = е-х от точки А (0; 1) до точки В (-1; е). Сделать чертеж.
Вариант 8
Задание 1.
Найти производные  данных функций.
данных функций.
а) 
|
б) 
|
в) 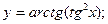
|
г) 
|
д) 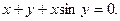
|
Задание 2.
Найти  и
и  для заданных функций: а) у = f (x); б) x =
для заданных функций: а) у = f (x); б) x =  (t), у =
(t), у =  (t).
(t).
а) у = e-x sin x; б) x = 2t – t3; y = 2t2.
Задание 3.
Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = ex, вычислить значение ea при а = 0,83, с точностью до 0,001.
Задание 4.
Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f (x) =  .
.
Задание 5.
В точках А и В, расстояние между которыми равно а, находятся источники света, соответственно с силами F1 и F2. На отрезке АВ наименее освещенную точку М0.
Замечание. Освещенность точки источником света силой F обратно пропорционально квадрату расстояния r ее источника света: E = kF/r2, k = const.
Задание 6.
Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.
а)  б)
б)  .
.
Задание 7.
Найти уравнения касательной, уравнение нормальной плоскости линии r = r (t) в точке t0.

Задание 8.
Дана функция z = f (x; y). Показать, что:
F  .
.
z =  F =
F = 
Задание 9.
Дана функция Z = F (x; y) и две точки А (x0; y0) и В (x1; y1). Требуется: 1) вычислить значение z1 в точке В; 2) вычислить приближенное значение `z1 функции в точке В, исходя из значения z0 функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, поучающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x0; y0; z0).
z = x2 – y2 + 5x + 4y; A (3; 2); B (3,05; 1,98).
Задание 10.
Дана функция z = f (x; y), точка А (x0; y0) и вектор  (а1; а2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора
(а1; а2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора  .
.
z = ln (3x2 + 4y2); A (1; 3); a (2; -1).
Задание 11.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а)  б)
б)  ; в)
; в)  г)
г) 
Задание 12.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 13.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 14.
Вычислить длину дуги полукубической параболы у = 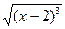 от точки А (2; 0) до точки В (6; 8).
от точки А (2; 0) до точки В (6; 8).
Задание 15.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
у6 = а2 (у4 – х4).
Задание 16.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = 1 – у2, x = у2, х = 2у2 + 1.
Задание 17.
Вычислить криволинейный интеграл

вдоль отрезка t = AB прямой от точки А (1; 2) до точки В (2; 4). Сделать чертеж.
Вариант 9
Задание 1.
Найти производные  данных функций.
данных функций.
а) 
|
б) 
|
в) 
|
г) 
|
д) 
|
Задание 2.
Найти  и
и  для заданных функций: а) у = f (x); б) x =
для заданных функций: а) у = f (x); б) x =  (t), у =
(t), у =  (t).
(t).
а) у = x  ; б) x = t + ln cos t; y = t – ln sin t.
; б) x = t + ln cos t; y = t – ln sin t.
Задание 3.
Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = ex, вычислить значение ea при а = 0,13, с точностью до 0,001.
Задание 4.
Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f (x) =  .
.
Задание 5.
Требуется изготовить закрытый цилиндрический бак объемом 6, 28 м3. Каким должны быть его радиус и высота, чтобы на изготовление бака ушло наименьшее количество листовой стали?
Задание 6.
Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.
а)  б)
б)  .
.
Задание 7.
Найти уравнения касательной, уравнение нормальной плоскости линии r = r (t) в точке t0.

Задание 8.
Дана функция z = f (x; y). Показать, что:
F  .
.
z =  F =
F = 
Задание 9.
Дана функция Z = F (x; y) и две точки А (x0; y0) и В (x1; y1). Требуется: 1) вычислить значение z1 в точке В; 2) вычислить приближенное значение `z1 функции в точке В, исходя из значения z0 функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, поучающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x0; y0; z0).
z = 2xy + 3y2 – 5x; A (3; 4); B (3,05; 3,95).
Задание 10.
Дана функция z = f (x; y), точка А (x0; y0) и вектор  (а1; а2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора
(а1; а2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора  .
.
z = 3x4 + 2x2y2; A (-1; 3); a (4; -3).
Задание 11.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а)  б)
б)  ; в)
; в)  г)
г) 
Задание 12.
Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.

Задание 13.
Вычислить несобственный интеграл или доказать его расходимость.

Задание 14.
Вычислить длину кардиоиды r = 3 (1 – cos  ).
).
Задание 15.
Вычислить с помощью двойного интеграла в полярных координат площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (а > 0).
(х2 + у2)2 = а2 (2х2+3у2).
Задание 16.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертеж данного тела и его проекции на плоскость х о у.
z = 0, z = 1 – х2, у = 0, у = 3 – х.
Задание 17.
Вычислить криволинейный интеграл

вдоль дуги t параболы у = 2х2 от точки О (0; 0) до точки А (1; 2). Сделать чертеж.
Вариант 10
Задание 1.
Найти производные  данных функций.
данных функций.
а) 
|
б) 
|
в) 
|
г) 
|
д)  . .
|
Задание 2.
Найти  и
и  для заданных функций: а) у = f (x); б) x =
для заданных функций: а) у = f (x); б) x =  (t), у =
(t), у =  (t).
(t).
а) у = xe-x  ; б) x = ln t; y =
; б) x = ln t; y =  .
.
Задание 3.
Применяя формулу Тейлора с остаточным членом в формуле Лагранжа к функции f (x) = ex, вычислить значение ea при а = 0,59, с точностью до 0,001.
Задание 4.
Найти наибольшее и наименьшее значения функции у = f (x) на отрезке [а; в].
f (x) = 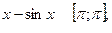
Задание 5.
Требуется изготовить открытый цилиндрический бак данного объема. Стоимость квадратного метра материала, идущего на изготовление дна бака, равно р1 руб., а стенок р2 руб. Каковы должны быть радиус дна и высота бака, чтобы затраты на материалы для его изготовления были наименьшими?
Задание 6.
Исследовать методами дифференциального исчисления функцию у = f (x) и используя результаты исследования, построить график.
а)  б)
б)  .
.
Задание 7.
Найти уравнения касательной, уравнение нормальной плоскости линии r = r (t) в точке t0.
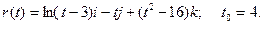
Задание 8.
Дана функция z = f (x; y). Показать, что:
F  .
.
z =  F =
F = 
Задание 9.
Дана функция Z = F (x; y) и две точки А (x0; y0) и В (x1; y1). Требуется: 1) вычислить значение z1 в точке В; 2) вычислить приближенное значение `z1 функции в точке В, исходя из значения z0 функции в точке А и заменив приращение функции при переходе от точке А к точке В дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции ее дифференциалом; 4) составить уравнение касательной плоскости к поверхности Z = F (x; y) в точке С (x0; y0; z0).
z =xy + 2y2 – 5x; A (1; 2); B (0,97; 2,03).
Задание 10.
Дана функция z = f (x; y), точка А (x0; y0) и вектор  (а1; а2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора
(а1; а2). Найти: 1) grad z в точке A; 2) производную в точке А по направлению вектора  .
.
z = 3x2y2 + 5xy2; A (-1; 1); a (2; 1).
Задание 11.
Найти неопределенные интегралы. В пункте а) и б) результаты проверить дифференцированием.
а)  б)
б)  ; в)
; в)  г)
г) 
Не нашли, что искали? Воспользуйтесь поиском: