Контрольная работа №2 1 страница

«Дифференциальные уравнения»

Вариант 1

Задание 1

Найти общее решение дифференциального уравнения:

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Материальная точка массой m = 2 г. погружается в жидкость, сила сопротивления которой пропорциональна скорости погружения с коэффициентом пропорциональности k = 0,002 кг/с. Найти скорость точки через 1 с. после начала погружения, если в начальный момент она была равна нулю.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 2

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

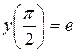
Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Моторная лодка двигалась в спокойной воде со скоростью км/ч. На полном ходу ее мотор был выключен, и через 10с скорость лодки уменьшилась до 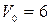км/ч. Сила сопротивления воды пропорциональна скорости движения лодки. Найти скорость лодки через 1мин после остановки мотора.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

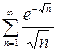
Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 3

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

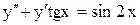Задание 4

Найти частное решение дифференциального уравнения 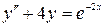, удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Пуля, двигаясь со скоростью , ударяется о достаточно толстую стену и начинает углубляться в нее, испытывая силу сопротивления стены, эта сила сообщает пуле отрицательное ускорение, пропорциональное квадрату ее скорости с коэффициентом пропорциональности . Найти скорость пули через после вхождения пули в стену.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

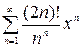
Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 4

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Материальная точка массой движется прямолинейно. На нее действует сила в направлении движения, пропорциональная времени с коэффициентом пропорциональности и сила сопротивления среды, пропорциональная скорости с коэффициентом пропорциональности . Найти скорость точки через 3 с после начала движения, если начальная скорость точки была равна нулю.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

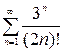
Задание 10

Исследовать сходимость знакопеременного ряда:

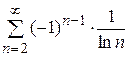
Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 5

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

В сосуде водного раствора соли. В сосуд втекает чистая вода со скоростью 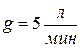, а смесь вытекает с той же скорость, причем перемешивание обеспечивает равномерную концентрацию раствора. В начальный момент в растворе соли. Сколько соли будет содержаться в сосуде через после начала процесса?

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 6

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Кривая проходит через точку и обладает тем свойством, что угловой коэффициент касательной в любой ее точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности . Найти уравнение кривой.

Задание 8

Найти общий член ряда:

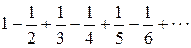
Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 7

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

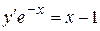
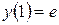
Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Кривая проходит через точку и обладает тем свойством, что произведение углового коэффициента касательной в любой ее точке на сумму координат точки касания равно удвоенной ординате этой точки. Найти уравнение кривой.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 8

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

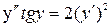Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Кривая проходит через точку и обладает тем свойством, что отношение ординаты любой ее точки к абсциссе пропорционально угловому коэффициенту касательной к этой кривой, проведенной в той же точке, с коэффициентом пропорциональности . Найти уравнение кривой.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл 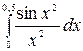с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 9

Задание 1

Найти общее решение дифференциального уравнения:

.

Не нашли, что искали? Воспользуйтесь поиском: