Контрольная работа №2 2 страница

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Кривая проходит через точку и обладает тем свойством, что отрезок, отсекаемый на оси ординат любой касательной, равен утроенной абсциссе точки касания. Найти уравнение кривой.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

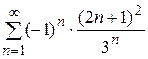
Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

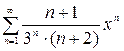
Задание 12

Вычислить определенный интеграл 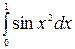с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения 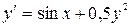, удовлетворяющего начальному условию .

Задание 14

Разложить функцию 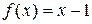в ряд Фурье на интервале .

Вариант 10

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

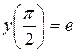
Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Кривая проходит через точку и обладает тем свойством, что отрезок, отсекаемый на оси абсцисс касательной, проведенной в любой точке кривой, равен кубу абсциссы точки касания. Найти уравнение кривой.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию 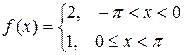в ряд Фурье на интервале .

Вариант 11

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Найти уравнение кривой, проходящей через точку и обладающей тем свойством, что отрезок любой касательной, заключенный между точкой касания и осью абсцисс, делится осью ординат пополам.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

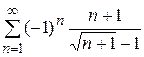
Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 12

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения 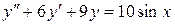, удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

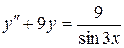
Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

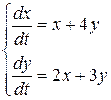
Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Найти уравнение кривой, проходящей через точку и обладающей тем свойством, что длина любой подкасательной равна среднему арифметическому координат точки касания (подкасательной называется проекция на ось Ох отрезка касательной, заключенного между точкой касания и точкой пересечения касательной с осью Ох).

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

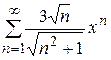
Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 13

Задание 1

Найти общее решение дифференциального уравнения:

.

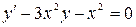Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Найти уравнение кривой, проходящей через точку и обладающей тем свойством, чтоугловой коэффициент касательной в любой точке кривой равен квадрату ординаты точки касания.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 14

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

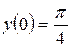
Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

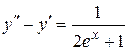
Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

В комнате, где температура 20⁰ С, некоторое тело остыло за 20 мин от 100⁰ С до 60⁰ С. Найти закон охлаждения тела. Через сколько минут оно остынет до 30⁰ С? Повышением температуры в комнате пренебречь.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

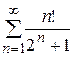
Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

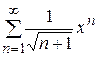
Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале .

Вариант 15

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

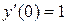Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

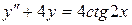
Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Тело массы m падает по вертикали с некоторой высоты без начальной скорости. При падении тело испытывает сопротивление воздуха, пропорциональное квадрату скорости тела. Найти закон движения тела.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения 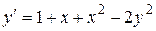, удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале , а - не целое число.

Вариант 16

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

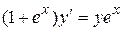
Задание 3

Найти общее решение дифференциального уравнения:

.

Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

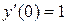Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Найти уравнение кривой, проходящей через точку , если угловой коэффициент касательной в любой точке кривой равен абсциссе точки касания.

Задание 8

Найти общий член ряда:

Задание 9

Исследовать сходимость числового ряда:

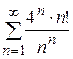
Задание 10

Исследовать сходимость знакопеременного ряда:

Задание 11

Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости:

Задание 12

Вычислить определенный интеграл 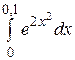с точностью до 0,001, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.

Задание 13

Найти три первых, отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения 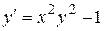, удовлетворяющего начальному условию .

Задание 14

Разложить функцию в ряд Фурье на интервале , а - не целое число.

Вариант 17

Задание 1

Найти общее решение дифференциального уравнения:

.

Задание 2

Найти решение задачи Коши дифференциального уравнения первого порядка

Задание 3

Найти общее решение дифференциального уравнения:

.

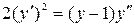Задание 4

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям: , .

Задание 5

Решить дифференциальное уравнение методом вариации произвольной постоянной

Задание 6

Дана система линейных дифференциальных уравнений с постоянными коэффициентами:

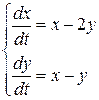
Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.

Задание 7

Найти уравнение кривой, проходящей через точку , если угловой коэффициент касательной к ней в любой точке кривой втрое больше углового коэффициента радиус-вектора точки касания.

Не нашли, что искали? Воспользуйтесь поиском: