
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Понятие о главных осях инерции плоских сложных фигур
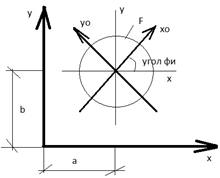
С – центр тяжести.
Оси, проходящие через центр тяжести – центральные оси
Через центр тяжести можно провести любое количество центральных осей
Две взаимно перпендикулярные оси, проходящая через центр тяжести являются главными, если центробежный момент инерции равен нулю (Ixy=0)
Ixy = F*ab
Положение главных осей определяется по формуле: tg2φ = -(2*Ixy/Ix – Iy); Ix>Iy
Оси симметрии симметричных фигур с двумя осями симметрии являются центральными осями и главными
Ось, проходящая через центр тяжести и перпендикулярная оси симметрии является главной осью(центральная по определению.)
S=0, Jxy=0
Осевые моменты инерции относительно главных осей называются главными моментами инерции.

Момент инерции (I) – площадь на квадрат расстояния
Момент инерции плоской сложной фигуры равен сумме моментов инерции всех входящих фигур относительно своей оси плюс сумма произведений площадей всех фигур на квадрат расстояния между центрами.
Ось, проходящая через центр тяжести и перпендикулярная оси симметрии является главной осью(центральная по определению.)
Оси, относительно которых центробежный момент инерции обращается в нуль, называются главными осями инерции. S=0, Jxy=0
Осевые моменты инерции относительно главных осей называются главными моментами инерции.
Момент инерции (I) – площадь на квадрат расстояния
Момент инерции плоской сложной фигуры равен сумме моментов инерции всех входящих фигур относительно своей оси плюс сумма произведений площадей всех фигур на квадрат расстояния между центрами.
Не нашли, что искали? Воспользуйтесь поиском: