Момент сопротивления поперечного сечения

Момент сопротивления - отношение момента инерции к расстоянию от центра тяжести до крайних точек

W=I/y, где W – момент сопротивления, I – момент инерции, y – расстояние от центра тяжести до крайних точек

Для нижней точки

Wн=I/yн

Для верхней точки

Wв=I/yв

34. Дифференциальные соотношения между изгибающим моментом, поперечной силой и внешней нагрузкой (неуверенна, но возможно это)

dM/dx=Q

произвольная поперечной силы

dQ/dx= - q

вторая произвольная моперечной силы

d²M/dx² = dQ/dx= - q для всех видов изгибов

где М – изгибающий момент, Q – поперечная сила, q - внешняя равномерно-распределённая нагрузка

35. Плоский поперечный изгиб. Внутренние усилия при плоском поперечном изгибе

Плоский поперечный изгиб -вид деформирования стержня, под действием поперечной нагрузки, лежащей в однйо плоскости (преимущественно в вертикальной плоскости).
Внутренние силы при плоскои поперечном изгибе:
- изгибающий момент (изгибает ось стержня)
- поперечная сила (действует перпендикулярн оси стержня в плоскости поперечного сечения).
При плоском поперечном изгибе возникают только вертикальные опорные реакции, горизонтальные усилия отсутсвуют.
Правило знаков.
Поперечная сила Q+полодительная, если вращается относительно рассматриваемой точки (сечения), по часовой стрелке.
Изгибающий момент (М) откладывается со стороны растянутого волокна и численно равен произведению силы на плечо и откладывается вниз отноистельно оси балки (положительно).
Q+ ниже оси балки откладывается. Q- откладывается выше оси балки.
Волокно - незримая, невесомоая, безрамерная нить или полоса.

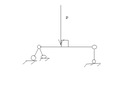
Плоский поперечный изгиб – это такой вид косого изгиба, при котором внешние силы действуют в одной плоскости.
При плоском поперечном изгибе силы в обязательном порядке перпендикулярны оси балки.
При поперечном изгибе все продольные силы отсутствуют.

При плоском поперечном изгибе внутренними усилиями являются:
Изгибающий момент — момент внешних сил относительно сечения балки
Поперечная сила-внутреннее усилие, возникающее в плоскости поперечного сечения стержня под действием нагрузки и стремящееся вызвать сдвиг одного поперечного сечения относительно другого, смежного с ним

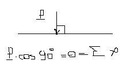
36. Понятие о плоском косом изгибе, внутренние силы при плоском косом изгибе.
плоский косой изгиб – это такой вид деформации стержня, при котором плоскости действия сил не совпадает ни с одной из главных осей инерции (пространственный, плоский)
Плоскость действия сил называется силовой плоскостью.
Линия пересечения силовой плоскости и поперечного сечения называется силовой линией.
Внутренние силы при плоском косом изгибе.
Являются изгибающий момент и поперечная сила.

37. Понятие о сдвиге, внутренние усилия при сдвиге

Сдвиг-один из видов одноостногонапряженного состояния,смещение одной части конструкции относительно другой под действием растягивающей или сжимающей силы
Плоскость контакта двух сопрягаемых элементов называется плоскостью сдвига.В качестве соединяемых элементов применяют:болты,шпитьки,заклепки,для стальных конструкций сварные соединения.
Возникают силы,осуществляющие смятие(силы смятия).По плоскости сдвига появляются силы среза,возникает срезающие напряжения
Внутренние силы при сдвиге обозначаются Тсм,Тср

Сдвиг - один из видов одноосного напряженного состояния, смещение одной части конструкции относительно другой под действием растягивающей или сжимающей силы

Плоскость контакта двух сопрягаемых элементов называется плоскостью сдвига. В качестве соединяемых элементов применяют: болты , шпильки , заклепки , для стальных конструкций сварные соединения.

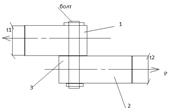
Под действием растягивающих сил происходит смещение

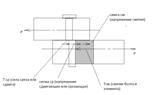
Напряженно-деформируемое состояние при сдвиге. Изменяется положение болта.

I. ∑х=0 Р-Тсм=0 Тсм=Р

II. ∑х=0 Тср-Тсм=0 Тср=Тсм=Р

Внутренние силы при сдвиге:

Силы смятия

Силы среза или сдвига (срезающие силы)

Напряжение

Тау – срезающее напряжение, сдвигающее напряжение

Тау = Тср/Аср=Р/Аср.

Аср – площадь среза

Сигма см. – сминающее напряжение (действующее напряжение)

Сигма см = т см/а см= р/ а см

А см- площадь смятия

Тау = Р/ А ср меньше равно R ср

Действующее напряжение не должно превышать определенной величины (Rср)

Предельно допустимое значение сопротивления материалов срезу называется расчетным сопротивлением материала на срез.

38. Понятие о моменте инерции, полярном и центробежном моментах инерции.

Момент инерции– площадь на квадрат расстояния.

Момент инерции плоской сложной фигуры равен сумме моментов инерции всех входящих фигур относительно своей оси плюс сумма произведений площадей всех фигур на квадрат расстояния между центрами.
Понятие о центробежном моменте.Ц.Б.равен произведению площади на расстояние от центра тяжести фигуры до соответствующих осей.
Понятие о полярном моменте интегральная сумма произведений площадей элементарных площадок на квадрат расстояния их от полюса — (в полярной системе координат), взятая по всей площади сечения.

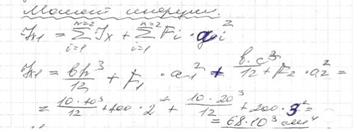
39. Внутренние усилия в поперечном сечении стержня (M,Q,N).

вопрос 39 тоже самое что 22
толоко рисунок другой

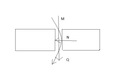
Внутренние усилия в элементе-изгибающий момент,нормальная сила N поперечная сила Q.
Эпюрами внутренних усилий называют графики, показывающие величины (а часто и знаки) соответствующих усилий в сечениях стержней. Эпюры строятся на продольных осях стержней как на нулевых линиях. На эпюрах продольных сил (эп. N), поперечных сил (эп.YQ,ZQ) и крутящих моментов (эп.tM) знаки ставятся. На эпюрах изгибающих моментов (эп. Y M и Z M) знаки, как правило, не ставятся, и ординаты (абсолютные величины изгибающих моментов в сечениях) откладываются со стороны растянутых волокон. При построении эпюр внутренних усилий рационально придерживаться следующего порядка. 1. Выбирается глобальная система координат X,Y,Z, в которой задаётся геометрия стержня, нагрузки и определяются опорные реакции. 2.Проводится разбиение стержня на грузовые участки. Под грузовым участком будем понимать такую протяжённость стержня, на которой выражения для внутренних усилий в сечениях не меняются. На участках (при целесообразности) выбираются дополнительные локальные системы координат Xi,Yi,Zi (i - номер грузового участка), облегчающие составление выражений для внутренних усилий. 3.С использованием метода сечений составляются аналитические выражения для внутренних усилий в сечениях на грузовых участках. При этом необходимо приводить расчётную схему выделенной части стержня, на которой показывать выбранную на участке систему координат и заведомо положительные внутренние усилия в текущем сечении. 4.По найденным выражениям строятся графики – эпюры внутренних усилий в сечениях стержня.

Не нашли, что искали? Воспользуйтесь поиском: