
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Аналитический способ сложения сил
Проекция равнодействующей сходящейся системы сил на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Пусть на тело действует система сил (F 1,…, F 4), при этом линии действия сил расположены в плоскости OXY (рис. 1.30).
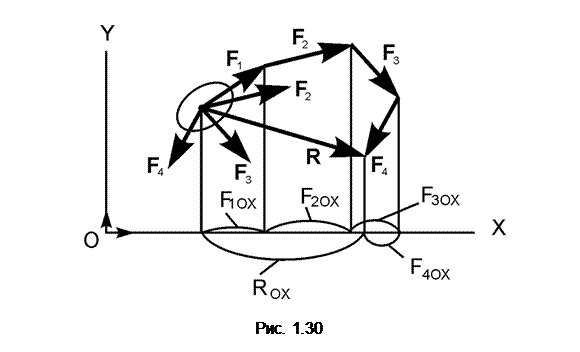 |
Их равнодействующая R = F 1 + … + F 4. Спроецируем составляющие векторы и их равнодействующую на ось OX. Очевидно F1OX > 0, F2OX > 0, F3OX > 0, F4OX < 0, ROX > 0.
Из рис. 1.30 видно, что ROX = F1OX + F2OX + F3OX + F4OX. Для любой сходящейся системы сил (F 1,…, F n), обозначая их равнодействующую через R, получим:
ROX = Σ FiOX;
ROY = Σ FiOY;
ROZ = Σ FiOZ.
Зная проекции ROX, ROY, ROZ равнодействующей R на координатные оси, можно найти её модуль и направляющие косинусы.
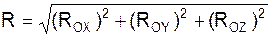 =
=  ;
;
cos(R, i) = ROX/R; cos(R, j) = ROY/R; cos(R, k) = ROZ/R.
Для плоской сходящейся системы сил последние выражения приобретают вид:
ROX = Σ FiОX; ROY = Σ FiОY;
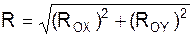 =
=  ;
;
cos(R, i) = ROX/R; cos(R, j) = ROY/R.
Известно, что сходящаяся система сил уравновешивается только в том случае, если их равнодействующая равна нулю. Графически плоская сходящаяся система сил изображается замкнутым силовым многоугольником (рис. 1.31).
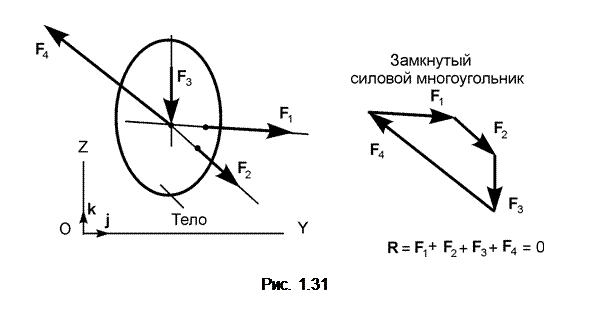 |
В общем случае
R = Σ F i = 0.
В замкнутом силовом многоугольнике все силы направлены в одну сторону по обходу многоугольника.
Частный случай. Три сходящиеся силы уравновешиваются, если треугольник этих сил замкнут.
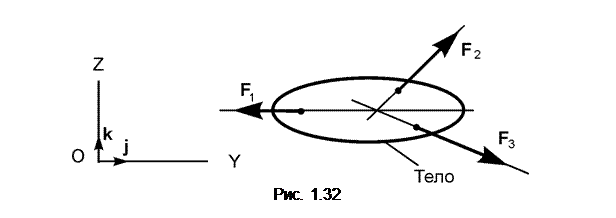
Линии действия трёх непараллельных, взаимно уравновешивающихся сил, лежащих в одной плоскости, пересекаются в одной точке (рис. 1.32).
Геометрическое условие равновесия сходящейся системы сил, расположенных в пространстве и на плоскости, одно и то же. Однако графический метод решения задач на равновесие сходящейся системы сил практически применяется только для плоской системы сходящихся сил.
Не нашли, что искали? Воспользуйтесь поиском: