На плоскую сходящуюся систему сил

Два стержня АС и ВС соединены шарнирно в узле С, к которому через блок D подвешен груз 1 весом 12 Н (рис. 1.33).

Определить реакции стержней АС, ВС, если угол a = 60^о.

Решение. Решаем задачу по изложенному алгоритму.

1.Выбираем правую систему отсчёта OYZ.

2.Вырезаем узел С и рассмотрим его равновесие. Активных сил к узлу С не приложено. Следовательно, Σ F _i^E = 0.

3.От узла С отбрасываем невесомые стержни АС и ВС и показываем реакции R _A и R _B. Эти реакции направлены вдоль стержней. Условимся рассматривать их растянутыми. Отбрасываем нить и показываем на рисунке реакцию Т нити. Нить растянута. Модуль Т реакции Т равен весу G груза 1.

4.На узел С действует плоская система сходящихся реакций связей. Поскольку Σ F _i^E = 0, то геометрическое условие равновесия приобретает вид Σ R _i^E = R _A + R _B + T = 0. Аналитические условия равновесия выражаются двумя уравнениями:

Σ 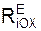= 0 = – R_A·sin(a) + R_B·cos(a) + T = 0; (1)

Σ 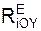= 0 = R_A·cos(a) + R_B·sin(a) = 0. (2)

5.Из уравнения (2) определим R_A = – R_B· = – R_B·tg(a). При подстановке R_A в уравнение (1) имеем

R_B·tg(a)·sin(a) + R_B·cos(a) + T = 0.

Откуда

R_B = – =

= – = – 6 Н.

Так как R_B < 0, то стержень ВС сжат.

R_A = – R_B·tg(a) = – (– 6)·1,732 = 10, 392 Н.

Так как R_A > 0, то стержень АС растянут.

Вопросы и задания для самоконтроля

1. Сформулировать определение термина «проекция силы на ось».

2. Записать формулы для определения проекций силы F на координатные оси декартовой системы отсчёта OXYZ.

3. Записать формулу для определения силы F через компоненты этой силы в декартовой системе отсчёта OXYZ.

4. Записать формулы для определения направляющих косинусов силы в декартовой системе отсчёта OXYZ.

5. Записать формулы для определения проекций равнодействующей системы сходящихся сил в декартовой системе отсчёта OXYZ.

6. Записать формулу, выражающую геометрическое условие равновесия сходящейся системы сил.

7. Записать уравнения равновесия для пространственной системы сходящихся сил в декартовой системе отсчёта OXYZ.

8. Записать уравнения равновесия для плоской системы сходящихся сил в декартовой системе отсчёта OXYZ.

Пара сил

Пару сил в механике рассматривают как одно из основных понятий, наряду с понятием силы.

Пара сил – система двух параллельных, противоположно направленных и равных по модулю сил, не лежащих на одной прямой.

Плоскость действия пары сил – плоскость, в которой находятся линии действия сил.

Плечо пары сил – кратчайшее расстояние (длина перпендикуляра) между линиями действия сил, составляющих пару сил.

На рис. 1.34 изображена пара сил, плоскость действия которой лежит в плоскости OXY системы отсчёта OXY.

Силы F ₁, F ₂ образуют пару сил. F₁ = F₂; F ₁ = – F ₂. Однако силы пары не уравновешиваются, так как они направлены не по одной прямой. Пара сил стремится произвести вращение тела, к которому она приложена. Действие пары сил на тело характеризуется её моментом.

Алгебраический момент пары сил – величина, равная взятому с соответствующим знаком произведению модуля одной из сил на её плечо.

M = ± F₁·h = ± F₂·h.

Алгебраический момент пары сил считают положительным, если пара сил стремится повернуть тело против вращения часовой стрелки, и отрицательным, если в сторону вращения часовой стрелки. В системе СИ момент пары сил измеряется в Н·м.

Момент пары сил – векторная мера механического действия пары сил, равная моменту одной из сил пары относительно точки приложения другой силы.

Момент пары сил изображается вектором М. Вектор момента М пары сил (F ₁, F ₂) направлен перпендикулярно к плоскости действия пары сил в сторону, откуда видно пару сил, стремящуюся вращать плоскость её действия в сторону, противоположную вращению часовой стрелки. Согласно определению (см. рис. 1.35), M ^ j, M ^ i, M = F₁×h = F₂·h. Таким образом, пара сил полностью характеризуется её моментом M.

Теорема. Пары сил, лежащие в одной плоскости, эквивалентны, если их алгебраические моменты численно равны и одинаковы по знаку.

Доказательство этой теоремы несложно и здесь оно не приводится.

Следствия из теоремы:

1.Пару сил, не изменяя её действия на тело, можно как угодно поворачивать и переносить в любое место плоскости её действия.

2.У пары сил можно изменять плечо и модуль силы, сохраняя при этом алгебраический момент пары и плоскость действия.

Суть теоремы и её следствий иллюстрируется рис. 1.36, на котором приведены пары сил с эквивалентными алгебраическими и векторными моментами. Плоскости действия пар сил совпадают с плоскостью YOZ.

Теорема. Пары сил в пространстве эквивалентны, если их моменты геометрически равны.

Доказательство этой теоремы также достаточно просто и здесь не приведено.

Из теорем о парах сил следует вывод: не изменяя действия пары сил на тело, пару сил можно переносить в любую плоскость, параллельную плоскости её действия, а также изменять её силу и плечо, сохраняя неизменными модуль и направление её момента.

Векторный момент пары сил, эквивалентный данной системе пар сил в пространстве, равен сумме векторных моментов заданных пар сил.

Не нашли, что искали? Воспользуйтесь поиском: