Справочный материал к заданию

Если для функции y = f (x) в точке х ₀ существует предел отношения приращения функции D f (x ₀) к приращению аргумента D x при условии D x ® 0, то этот предел называют производной функции y = f (x) в точке x ₀ и обозначают f ¢(x ₀) или y ¢(x ₀), т.е.

Где .Существуют и другие обозначения производной. Например . Нахождение производной называют дифференцированием.

Пусть U (x) и V (x) — дифференцируемые функции, C — const, тогда правила нахождения производных имеют вид:

1. (U ± V)¢ = U ¢

2. (U · V)¢ = U ¢· V + U · V ¢;

3. (C U)¢ = CU ¢;

4. ;

5. [ U (V (x))]¢ = ;

6. (U ^V)¢ = V · U^{V -1} · U ¢+ U ^V · ln U · V ¢.

Если y = f (x) имеет производную f ¢(x) ¹ 0, то обратная функция
x = f ^--1(y) в соответствующей точке имеет производную, причем .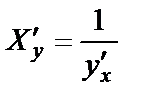

Если функция задана параметрически, т.е.

где t — параметр и х ¢(t) ¹ 0, то .

Правила дифференцирования основных элементарных функций приведены в следующей таблице:

Не нашли, что искали? Воспользуйтесь поиском: