Пример решения задачи

1) y = ln⁵sin(6 x + 3); 2) y = ; 3) x – y = arcsin x – arcsin y;

4) x = cos²3 t

y = ln(t ³ + 1).

1) Вычислим производную сложной функции, где y = U ⁵; U = lnV;

V = sin j; j = 6 x + 3, т.е.

Можно не вводить дополнительные обозначения, определив количество промежуточных функций и перемножить их производные.

2) Вычислим производную показательно-степенной функции двумя способами:

а) Используя правило 6-е дифференцирования функций, получим:

б) Используем логарифмическое дифференцирование. Для этого логарифмируем данную функцию: ln y = ln(cos x) или ln y = (x ² – 3) · ln cos x; и дифференцируем полученное выражение (слева производная сложной функции, справа производная произведения)

Следовательно, y ¢ = y · (2 x · ln cos x – (x ² – 3) ·tg x) или

y ¢ =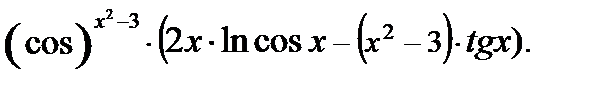

3) Вычислим производную неявной функции. Для этого дифференцируем обе части равенства по переменной х, считая у функцией от x, получим:

Решим уравнение относительно .

4) Вычислим производную функции, заданной параметрически. Для этого найдем 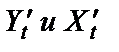и воспользуемся формулой :

Получим .

Не нашли, что искали? Воспользуйтесь поиском: