Визначення ретикулярних щільностей атомних площин кристала

Кристал, або кристалічна структура, — це пакет паралельних рівновіддалених одна від одної атомних площин. Просторове орієнтування таких площин, на які можна подумки розбити той самий кристал, може бути найрізноманітнішим. На рис. 2.7 представлені фрагменти сімейств таких паралельних площин. Порівнюючи різні сімейства площин, можна довести, що зміна їхнього просторового орієнтування супроводжується відповідною зміною заселеності цих площин і відстаней між сусідніми атомними площинами. Переходячи від фрагменту а до фрагменту д, можна помітити, як зі зменшенням міжплощинних відстаней зростає відстань між сусідніми атомами в кожній атомній площині й, отже, зменшується заселеність відповідних атомних площин.

Параметр, що характеризує заселеність атомних площин, одержав назву ретикулярної (або атомної) щільності. Він виражається кількістю атомів, що припадають на одиницю площі відповідної атомної площини. За законом Браве природне огранування кристала утвориться гранями з максимальною ретикулярною щільністю. Треба враховувати, що закон Браве має статистичний характер, тобто виражає загальну тенденцію кристалоутворення, і може мати деякі відхилення в окремих випадках.

Відзначимо один з досить важливих наслідків із закону Браве. Якщо грані кристала характеризуються порівняно високими значеннями ретикулярних щільностей, то лінії їхнього перетинання - ребра кристала - являють собою атомні ряди з порівняно (з іншими атомними рядами) високою щільністю атомів (на одиницю довжини). Звідси випливає досить важливий наслідок, що координатні осі (або, як їх ще називають, кристалографічні осі) представлені найбільш щільними атомними рядами.

Значення закону Браве не обмежується характеристиками елементів природного огранування кристалів - його граней і ребер, він охоплює більш широку сферу явищ. Класифікуючи атомні площини за їхньою заселеністю - по ретикулярною щільністю, закон Браве дозволяє розділити атомні площини кристалу на щільнозаселені, які чинять основний, визначальний вплив на властивості кристалу, і на малозаселені атомні площини, які чинять на властивості кристала лише незначний вплив.

Як приклади розглянемо визначення ретикулярних щільностей деяких металевих фаз. На рис.2.8 наведений кубічний елементарний осередок α-заліза. Величина площі грані куба (рис. 2.8 а) дорівнює а ². Кількість атомів, які припадають на цю площу, підрахуємо, з огляду на те, що кожний атом, що перебуває у вершині квадрата грані, одночасно належить чотирьом квадратам і, отже, на один квадрат буде припадати від кожного такого верхового атома всього по 1/4. Отже, на цілий квадрат припадає всього один атом, і тоді значення ретикулярної щільності для розглянутої грані куба складе 1/ а ².

Рисунок 2.7 - Різні сімейства (а - д) паралельних атомних площин кристала

Для іншої атомної площини кристалічної структури — α-заліза, що обмежена парою паралельних ребер куба й парою діагоналей граней куба — називаємо її діагональною площиною куба (рис. 2.8, б), розрахунок ретикулярної щільності аналогічний. Площа діагонального перетину куба дорівнює , що відповідає числу атомів куба складе . Ретикулярна щільність дорівнює . Отже, ретикулярна щільність діагональної атомної площини кубічної кристалічної структури α-заліза перевищує таку для грані того ж куба в 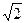раз.

І нарешті, зрівняємо отримані результати із третьою атомною площиною в тому ж кристалі, що проходить через три вершини куба перпендикулярно до його об'ємної діагоналі (рис. 2.8 в). Відповідний перетин куба має форму рівностороннього трикутника зі стороною . Площа цього трикутника дорівнює . Трохи складніше справа з підрахунком кількості атомів, що припадають на площу цього трикутника. Кожний із трьох атомів, що перебувають у вершинах цього структурного трикутника, «віддає» цьому трикутнику лише 1/6 частину, оскільки інші 5/6 частин кожного атома при вершині будуть належати іншим п'яти суміжним структурним рівностороннім трикутникам, тому що кут при вершині кожного рівностороннього трикутника дорівнює 60°. Таким чином, число атомів, що припадають на площу розглянутого рівностороннього трикутника, складе всього атома. У результаті одержимо для цієї атомної площини значення ретикулярної щільності

Рисунок 2.8 - До визначення ретикулярних щільностей у кристалічній структурі α-Fе: а - вертикальна координатна атомна площина (100); б — вертикальна діагональна атомна площина (110); в — похила атомна площина (111)

Тепер можна провести порівняння отриманих величин ретикулярних щільностей для трьох розглянутих атомних площин у кристалічній структурі α-заліза, використовуючи для цього відношення відповідних чисельних значень і розташовуючи атомні площин у тому самому порядку (1,00:1,41:0,82). Таким чином, одержуємо максимальну ретикулярну щільність для діагональної атомної площини α -заліза (рис.2.8 б) і мінімальну (для трьох порівнюваних атомних площин) для останньої з розглянутих площин, що проходить через три вершини куба (рис.2.8 в).

Проведемо також порівняння ретикулярних щільностей для іншої кристалічної структури — кубічної структури міді (рис.2.9), де атоми займають положення у вершинах кубічного елементарного осередку й у центрах її граней. Почнемо з атомної площини, що збігається із гранню елементарного осередку (рис. 2.9 а). Площа грані куба дорівнює а ². Кількість атомів, що припадають на цю площу, дорівнює двом, враховуючи, крім чотирьох атомів по вершинах квадрата, кожний з яких вносить по 1/4 (як у структурі α-заліза), ще й один атом у центрі квадрата. Отже, ретикулярна щільність розглянутої атомної площини дорівнює

Рисунок 2.9 - До визначення ретикулярних щільностей у кристалічній структурі Си: а-а- вертикальна координатна атомна площина (100); б — вертикальна діагональна атомна площина (110); в — похила атомна площина (111)

Для діагональної атомної площини кристалічної структури міді (рис. 2.9 б) площа прямокутного перетину куба елементарного осередку дорівнює . При розрахунку кількості атомів, що припадають на зазначену площу, крім «кутових» атомів, врахуємо також два атоми, що перебувають у центрах передньої й задньої граней куба, кожний з яких вносить у розглянутий прямокутний перетин по половинці, тобто . Отже, для діагональної атомної площини кристалічної структури міді одержимо значення ретикулярної щільності .

Для третьої атомної площини (рис. 2.9 в), що проходить через вершини кубічного елементарного осередку, площу рівностороннього трикутника визначимо за аналогією до попередньої кубічної структури α-заліза як

При підрахунку кількості атомів, що припадають на площу структурного трикутника, врахуємо, крім трьох атомів у вершинах трикутника, кожний з яких вносить по 1/6 своєї частини (за аналогією до попередньої структури α-заліза), також три атоми, розташовані по центрах ребер рівностороннього структурного трикутника, кожний з яких віддає розглянутому трикутнику по половинці: . У результаті одержимо для даної атомної площини значення ретикулярної щільності .

Порівняємо тепер отримані чисельні значення ретикулярних щільностей у порядку їхнього розгляду (2,00:1,41:3,27). Як бачимо, у кристалічній структурі міді найбільш щільнозаселеною виявилася атомна площина, що проходить через три вершини кубічного елементарного осередку (рис. 2.9 в), а самою малонаселеною - друга (діагональна) атомна площина (рис. 2.9 б).

На підставі отриманих даних було б необережним прогнозувати, якими саме гранями буде покритий кристал міді, оскільки, як про це уже неодноразово згадувалося, природне огранування кристала досить мінливе і залежить від безлічі різноманітних факторів (а не тільки від ретикулярної щільності), а сам закон Браве за своїм змістом має статистичний характер.

Корисними можуть виявитися також розрахунки ретикулярних щільностей для кристалічної структури магнію (рис.2.10 а), де атоми розташовуються паралельними горизонтальними трикутними шарами таким чином, що перший шар повторюється третім шаром, основа елементарного осередку мають форму ромба (із двох рівносторонніх трикутників зі стороною а), а другий шар, що перебуває посередині між основами на висоті , зміщений стосовно основ на величину 1/3 великої діагоналі ромба.

Для базисної площини основи гексагональної призми (рис. 2.10 а) величину ретикулярної щільності визначимо, розділивши три атоми (кожний атом біля вершини гексагона вносить у цей гексагон по одній третині плюс атом у центрі гексагона, тобто 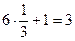) на площу гексагона , і одержимо в результаті величину .

Для похилої площини (рис. 2.10 б) віднесемо 1,5 атома до площі трапеції (прийнявши відношення = 1,633) і одержимо значення ретикулярної щільності .

Для вертикальної площини (рис. 2.10, а) віднесемо єдиний атом (кожний із чотирьох атомів біля вершин прямокутної грані приносить по одній чверті) до площі прямокутника ас = 1,633 а ² і одержимо значення ретикулярної щільності .

Таким чином, зіставлення розрахованих значень ретикулярної щільності для різних атомних площин кристалічної структури магнію показує значна перевага горизонтальної базисної атомної площини в порівнянні з іншими площинами.

Для багатьох теоретичних оцінок порівняння ретикулярних щільностей різних атомних площин кристала може становити значний інтерес.

Висновки. Слідом за розгорнутим аналізом зовнішнього огранування кристалів і перерахуванням простих форм і деяких їхніх комбінацій розглянуті деякі найважливіші закони кристалографії, які дозволяють пояснити причини мимовільного природного огранування кристалів з позицій так званої граткової теорії.

Якщо закон Гаюї дозволив уперше встановити періодичну внутрішню будову кристалів, то Вейсом були розроблені основні принципи математичного моделювання кристалічних структур, а Браве, затверджуючи граткову теорію будови кристалів, розробив конкретні прийоми вибору координатних систем для опису просторового розташування атомів у кристалах, де роль природних осей координат виконують найщільніші атомні ряди.

Застосування системи спеціальних критеріїв для опису кристалічних структур дозволяє використовувати стандартні умови для вибору відповідних координатних систем. Використання кількісної оцінки заселеності атомних площин за допомогою так званих ретикулярних щільностей дозволяє оцінити роль структурного фактора у формуванні властивостей кристала.

Для виявлення щільнозаселених атомних площин порівнюють значення ретикулярних щільностей різних атомних площин кристала (кількість атомів, що припадають на одиницю площі даної атомної площини) і відбирають за відповідними максимальними значеннями.

Рисунок 2.10 До визначення ретикулярних щільностей у кристалічній структурі Мg: а-горизонтальна атомна площина (0001); б- похила атомна площина () і вертикальна атомна площина ()

Не нашли, что искали? Воспользуйтесь поиском: