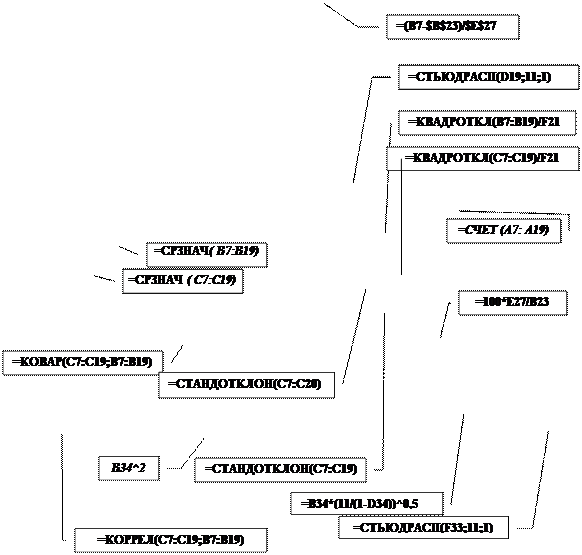
Величина коефіцієнта варіації свідчить про кількісну однорідність статистичної сукупності об’єктів , що вивчається.

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

3). Тісноту кореляційного зв’язку між двома економічними ознаками.

Для з’ясування наявності лінійної кореляційної залежності між Y і X можна використати коефіцієнт парної кореляції. , значення якого обчислюється в комірці B34 з використанням статистичної функції, в результаті отримаємо =0,991055546.

Коефіцієнт приймає значення від (-1) до (+1) включаючи (0).

В останньому випадку змінні є незалежними, якщо:

- зв'язок є слабким;

- зв'язок є середнім;

- зв'язок вважається тісним.

Величина коефіцієнта кореляції =0,991055546 свідчить, що залежність між показниками Y і X висока, можна будувати просту регресію.

4). Статистичну надійність знайденого зв’язку між ознаками.

Вибірковий коефіцієнт кореляції, здобутий за вибірковими даними, є точковою оцінкою коефіцієнта кореляції, випадковою величиною. Тому доцільно зробити перевірку гіпотези про відсутність кореляційного зв’язку. Для цього перевіряється нульова гіпотеза 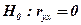і альтернативна гіпотеза

.

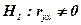Припустимо, що двомірна випадкова величина розподілена за нормальним законом. Для вибірки обчислюється статистика

, (12), яка має розподіл Сьюдента з рівнем значущості і k=N - 2 ступенями вільності.

Для заданої ймовірності p і k ступенів вільності:

¨ обчислимо в комірці F33 по формулі (12) значення t, в результаті отримаємо t=24,63064196;

¨ визначимо в комірці F34 p - значущість при односторонній перевірці 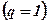для розрахункової величини t=24,6306419, з урахуванням числа ступенів вільності k=11, в результаті отримаємо p=2,83243E-11;

¨ порівняємо з обраним рівнем значущості .

Оскільки згідно з загальною схемою перевірки статистичних гіпотез (рис.2), фактична ймовірність помилки 1 роду попадає в критичну область 2,83243E-11<0,5, то нульова гіпотеза відхиляється і з достовірністю 0,9999999 можна стверджувати, що справедлива альтернатива , тобто прямий кореляційний зв'язок між Х і У є високо надійним. Статистично значущім.

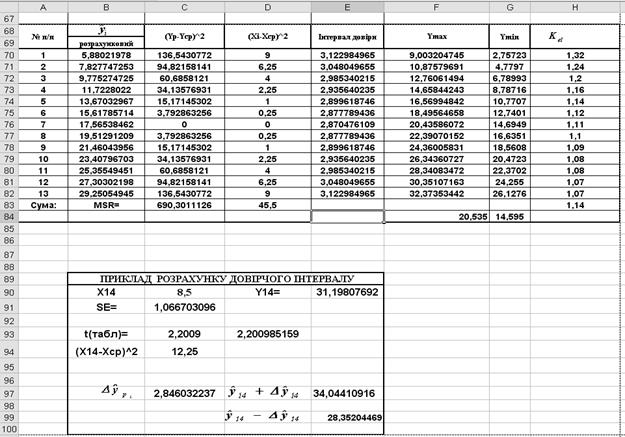
Таблиця 4

Оцінка параметрів лінійної регресії 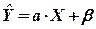, (початок)

3). Побудуємо рівняння парної регресійної моделі. Дамо економіко - статистичну та геометричну інтерпретацію коефіцієнтів регресії, (табл.4, продовження 1).

На попередньому апріорному техніко - економічному аналізі (за даними таблиці 3), введені основні ймовірності припущення щодо лінійної моделі .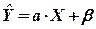

Визначимо чисельні значення невідомих коефіцієнтів і 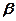парної лінійної моделі (2) з застосуванням редактора Excel декілька способами, а саме:

1). За допомогою метода найменших квадратів, з використанням коефіцієнтів коваріації та варіації, з цією метою обчислимо:

¨ в таблиці 4, початок:

значення коваріації 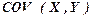, в результаті отримаємо 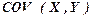=13,63269231, (комірка C29);

значення варіації 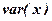(9), в результаті отримаємо 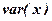= 3,5, (комірка E25).

Коли переважна більшість добутків відхилень має однаковий знак (пряма залежність між змінними) коваріація позитивна. Коли переважна більшість добутків відхилень має різні знаки (зворотна залежність між змінними) коваріація негативна. У разі взаємної компенсації добутків різних знаків говорять про відсутність або слабку залежність між Y і X;

¨ в таблиці 4, продовження 1:

значення коефіцієнта регресії , в результаті отримаємо =3,895054945, (комірка B39);

значення коефіцієнта регресії , в результаті отримаємо 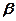= -1,90989011, (комірка D39).

2). За допомогою вбудованої функції “ЛИНЕЙН ”, дляцього потрібно:

під вихідними даними активізувати розрахунковий блок комірок, розміру 5х2 (C41:C45;D41:D45);

обчислити значення в комірці C41 з використанням вбудованої статистичної функції “ЛИНЕЙН”;

натиснути на комірці C41 клавішу F2, потім сумісно комбінацію .

Таблиця 4

Оцінка параметрів лінійної регресії 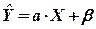(продовження 1)

Отримаємо в комірках C41:C45;D41:D45 розрахункові дані, (із справа на ліво):

у першому рядку – коефіцієнти парної лінійної регресі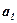ї і ;

у другому рядку - стандартні помилки відповідних коефіцієнтів парної лінійної регресії;

у третьому рядку стандартна помилка усього рівняння регресії та коефіцієнт детермінації;

у четвертому рядку - число ступенів вільності та розрахункове значення F-критерію Фішера;

у п’ятому рядку сума квадратів відхилень фактичних спостережень

від та сума квадратів відхилень фактичних спостережень від середнього

значення .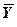

Таблиця 4

Оцінка параметрів лінійної регресії 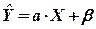(продовження 2)

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: