З ймовірністю 95% можливо стверджувати, що істинні значення розрахункових коефіцієнтів регресії знаходяться у вказаних вище інтервалах.

⇐ Предыдущая 5 6 7 8 9 10 111213 14 Следующая ⇒

Адекватності.

Показником адекватності отриманого рівняння емпіричним даним є коефіцієнт автокореляції залишків першого порядку.

Автокореляція – це кореляція змінної Х з цією ж змінною, але зрушеною на k спостережень, які називають лагом. Лаг визначає порядок коефіцієнта автокореляції.

Якщо залишки регресійної моделі для кожного спостереження позначити як , то на їх основі коефіцієнт автокореляції залишків першого порядку визначається так: .

Позитивна і статистично значуща величина свідчить про “недовантаженість ” регресійної моделі – потрібно ввести в рівняння додаткові важливі чинники чи ускладнити форму зв’язку.

Негативно і статистично значуща величина свідчить про “перевантаженість ” регресійної моделі – потрібно виключити з рівняння зайві чинники чи спростити форму зв’язку.

Якщо виконується умова r(1)=0, тобто абсолютна величина коефіцієнту автокореляції залишків першого порядку мала і він статистично незначущий – то регресійну модель можна вважати адекватною соціально-економічному явищу, що вивчається.

Для визначення адекватності рівняння регресії 1,90989011+ 3,895054945Х з використання вбудованого блока КРА необхідно:

¨ Вивести діалогове вікно для отримання результату КРА (команди вивода описані раніше).

¨ Активізувати віконце “ Остатки ”, при цьому вказати адреси комірок Y, адреси комірок Х, рівня надійності (95%), виводом результатів на новий робочий лист.

Після команди “OK” на новому листі з’явиться таблиця з інформацією, (табл.6. Залишки регресійної моделі), в якої наводяться розрахункові значення результативної ознаки та залишки , що не можуть бути пояснені за допомогою рівняння (13).

Таблиця 6

Залишки регресійної моделі

¨ Побудувати коефіцієнт автокореляції залишків першого порядку r(1) і перевірити його статистичну значущість.

Для цього необхідно повторити процедуру КРА, в якій у ролі результативної ознаки буде виступати вихідний ряд залишків (табл.6), скорочений на одиницю, у ролі чинника – ряд залишків, зрушений на одне спостереження.

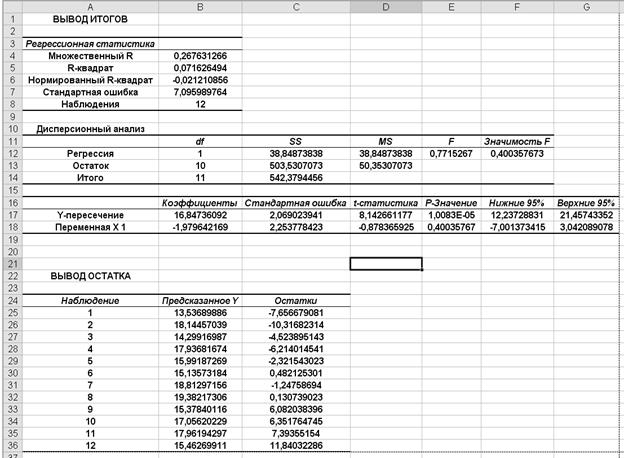
Результати вихідних даних для розрахунку r(1) наведені в таблиці 7, де r(1)=0,267631266 - показник ”Множественный R” є коефіцієнтом автокореляції залишків першого порядку, (поз.1) ;

p=0,400357673 - показник, який визначає фактичну значущість, (поз.2).

Згідно з загальною схемою, рис.3 рівень p- значущості коефіцієнта автокореляції залишків першого порядку потрапляє в область припустимих значень (0,400357673>0,05) і нульова гіпотеза не відхиляється.

Регресійну модель “ - 1,90989011+ 3,895054945 Х ” можна вважати такою, що адекватно описує залежність прибутку фірми від витрат витрачених для отримання прибутку.

Таблиця 7

Вихідні дані для розрахунку r(1)

4. Практичне застосування парної лінійної моделі,

(див. табл. 4, продовження 2)

Після побудови рівняння регресії, що адекватно описує економічний об’єкт дослідження, переходимо до його використання в наступних напрямках.

Надаємо характеристику середньому рівню результативної ознаки при 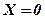за допомогою коефіцієнта регресії (розглянуті раніше, в прикладі п.2.5).

1). Надаємо характеристику середнього абсолютного впливу чинника на результативну ознаку за допомогою коефіцієнта регресії , (розглянуті раніше, в прикладі, п.2.5).

2). Надаємо характеристику середнього відносного впливу чинника на результативну ознаку за допомогою коефіцієнта еластичності,

де значення - обчислюється в комірках B25 і B23 відповідно (табл.4, початок);

- коефіцієнт регресії (табл. 4, комірка В39, продовження 1).

Звідси

,

Коефіцієнт еластичності показує, що з ростом вкладених витрат на виробництво у 1,01 рази прибуток фірми підніметься в середньому на 1,109%.

Коефіцієнт еластичності для базисних значень та прогнозу обчислюється у діапазоні комірок H70:H82.

3). Отриману адекватну модель (13) використаємо як інструмент прогнозу:

¨ з використанням точкового прогнозу, який дає значення результативної ознаки для відповідного рівня (наприклад: ).

Для витрат в сумі 8,5 тис. грн. середнє значення прогнозу отриманого прибутку 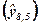складе:

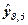= -1,90989011 + 3,895054945 * 8,5=31,20 тис. грн.,

Тобто, при рівні витрат в сумі 8,5 тис. грн. слід очікувати отримання прибутку в сумі 31,20 тис. грн.;

¨ з використанням довірчого інтервалу для окремого значення .

Довірчий інтервал прогнозу будується на основі загального співвідношення , де - гранична помилка прогнозу.

, (15)

= 2,846032237, (комірка ).

де - середня квадратична (стандартна) помилка регресії, розраховується автоматично при використанні другого і третього методів знаходження коефіцієнтів регресії, (табл.5. Результати КРА).

Розрахунки приведені в блоці комірок .

Для значення фактора 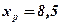середнє значення прогнозу показника з надійністю буде знаходиться у межах від 28,35 до 34,05 ()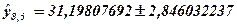

Таким чином можна стверджувати, що при незмінних для даної сукупності обставин з збільшенням вкладання витрат на виробництво, буде супроводжуватися і ріст прибутку фірми;

¨ з використанням довірчого інтервалу математичного сподівання значення .

В блоках комірок приведені розрахунки для побудови довірчої зони для базисних даних і прогнозу , для всієї сукупності спостережень (), де

гранична помилка прогнозу () розраховується по формулі:

.

5. Побудуємо графік лінії регресії для базисних даних та прогнозу.

Для остаточного вирішення питання про форму зв’язку у випадку парної регресії, наочного уявлення одержаних розрахунків будуємо графіки (рис.6) фактичних даних , лінії регресії для базисних даних та прогнозу , довірчу зону для базисних даних і прогнозу , коефіцієнта еластичності .

Для побудови графіка моделі у діалоговому вікні Майстер діаграм вибираємо тип діаграми відповідно рис.4, а далі від 1 шага до 4 шага (рис.5) будуємо перелічені раніше графіки залежності (рис.6).

Рис.4.Диалогове вікно типів діаграм

Рис.5.Мастер діаграм

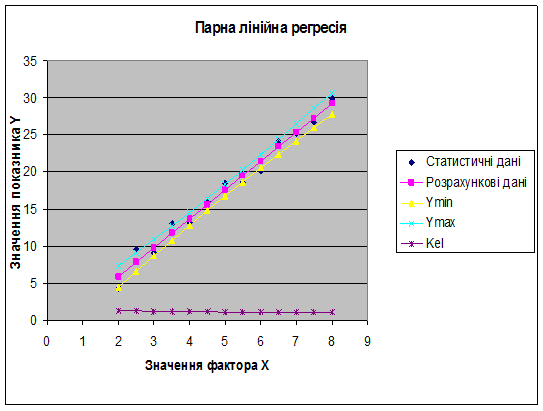
Рис.6 Графік парної лінійної регресії - 1,90989011+ 3,895054945 Х

Згідно графіка парної лінійної регресії (рис.6) надаємо остаточний висновок, що залежність між значеннями фактора і показника є лінійною.

Значення коефіцієнта еластичності під час зростання фактора від 2 до 8, спадає від 1,32 до 1,07.

⇐ Предыдущая 5 6 7 8 9 10 111213 14 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: