Евклидово пространство.

Определение: Линейное пространство называется евклидовым, если в нем введена операция скалярного произведения, которая ставит в соответствие любым векторам х и у Є L число x•y, удовлетворяющее следующим свойствам:

1° x•y=y•x;

2° (lx)• y= l(x•y);

3° x•(y + z)= x•y + x•z;

4° x • x ³ 0,причем скалярный квадрат x•x= 0 ↔ х= 0.

В Евклидовых пространствах можно ввести понятие длины вектора (модуль вектора) 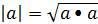и угол между векторами .

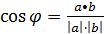Нужно показать, что ï cos j ï£ 1.

Для этого докажем неравенство Коши - Буняковского (Шварца):

0£│a • b│£│a│·│b│.

Док-во: Рассмотрим скалярный квадрат

(a- lb)•(a- lb)= a • a- la • b- l a • b + l²b • b= │a│²- 2la • b+ l²│b│²³ 0, как скалярный квадрат.

Последнее неравенство рассмотрим как квадратное относительно l.

l²│b│²- 2λa•b +│a│²³ 0.

Чтобы это неравенство выполнялось при любом λ, нужно, чтобы дискриминант D£ 0.

D= b²- 4ac= (-2a•b)²- 4│b│²·│a│²£ 0.

4(a•b) ²- 4│b│²·│a│²£ 0 ê: 4;

(a•b) ²£ │b│²·│a│².

Извлекаем корень :

0£│a • b│£│a│·│b│.

Ч.т.д.

На основании неравенства Коши - Буняковского определение косинуса угла между векторами Евклидова пространства корректно.

Замечание: Евклидово пространства размерности n принято обозначать Eⁿ,

E² - евклидово пространство всех векторов на плоскости, E³ - в пространстве.

Не нашли, что искали? Воспользуйтесь поиском: