Скалярное произведение векторов в ортонормированном базисе.

Определение: Два вектора Евклидова пространства называются ортогональными, если их скалярное произведение равно нулю.

Определение: Базис Евклидова пространства l₁, l₂,...,l_n называется ортонормированным, если векторы l₁, l₂,...,l_n попарно ортогональны и длина каждого вектора равна 1, т.е.

.

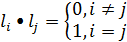Пусть вектора x, y заданы своими координатами в ортонормированном базисе l₁, l₂,...,l_n:

х =(α_1, α_2,… α_n)= α₁ l₁+ α₂ l₂+... +α_n l_n, у = (β_1, β₂, … β_n)= β₁ l₁+ β₂l₂+…+β_n l_n.

Найдем их скалярное произведение:

x•y=(α_1, α_2,… α_n)•(β_1, β₂, … β_n)= (α₁ l₁+ α₂ l₂+... +α_n l_n)•(β₁ l₁+ β₂l₂+…+β_n l_n)=

= α₁ l₁ •β₁ l₁+ α₁ l₁ •β₂l₂+…+ α₁ l₁ •β_n l_n+ α₂ l₂ •β₁ l₁+ α₂ l₂ •β₂l₂+…+

+α₂ l₂ •β_n l_n+…+ α_n l_n •β₁ l₁+ α_n l_n •β₂l₂+…+ α_n l_n •β_n l_n=

= α₁ β₁ (l₁ • l₁)+ α₁ β₂(l₁ •l₂)+…+ α₁ β_n (l₁ •l_n)+ α₂ β₁(l₂ •l₁)+ α₂ β₂(l₂ •l₂)+…+

+ α₂ β_n (l₂ •l_n)+…+ α_n β₁(l_n •l₁)+ α_n β₂(l_n •l₂)+…+ α_n β_n(l_n •l_n)=

=(учтем, что вектора l₁, l₂,...,l_n – ортонормированный базис)=

= α₁ β₁+ α₂ β₂+…+ α_n β_n.

Т.о. скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат.

Не нашли, что искали? Воспользуйтесь поиском: