
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Оптимизация комплекса работ по времени
Оптимизация комплекса операций по времени сводится к сокращению продолжительности критического пути. Необходимость проведения оптимизации сетевого графика по времени возникает тогда, когда критическое время выполнения комплекса операций превосходит срок T0, на котором настаивает ЛПР. Очевидно, подобная задача требует проведения определенных мероприятий и (или) вложения дополнительных средств.
Иногда оптимизация достигается за счет перепланировки сетевого проекта (изменения топологии сети). Например, одновременно выполняемые операции, имеющие резервы времени и не лежащие на критическом пути, могут выполняться последовательно (если это допускается технологией). Освободившиеся при этом ресурсы можно использовать на критических операциях, что ускорит их выполнение. Сокращение времени выполнения операций возможно также за счет автоматизации производственных процессов, улучшения организации работ, использования передовых технологий и т.д.
Оптимизация комплекса операций по времени может проводиться с привлечением дополнительных средств и с использованием внутренних резервов.
Приведем математическую формулировку процесса оптимизации по времени.
Пусть задан сетевой график выполнения комплекса операций. Время выполнения каждой операции равно tij. Пусть также вложение дополнительных средств в операцию сокращает время выполнения с tij до t’ij. Естественно, для каждой операции существует минимально возможное время ее выполнения, равное dij. Требуется определить время начала и окончания выполнения операций, а также величину дополнительных средств xij, которые необходимо вложить в каждую из операций (i, j), чтобы общее время выполнения комплекса операций было минимальным. При этом сумма вложенных дополнительных средств не должна превышать заданной величины c, а время выполнения каждой операции должно быть не меньше минимально возможного времени dij.
Математически условия задачи можно записать следующим образом:
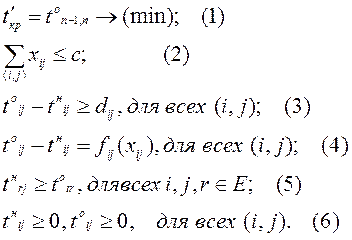
Ограничение (2) определяет сумму вложенных дополнительных средств: она не должна превышать величины c. Ограничения (3) показывают, что продолжительность каждой работы должна быть не менее минимально возможной ее продолжительности. Ограничения-равенства (4) показывают зависимость продолжительности каждой работы от вложенных в нее дополнительных средств. Ограничения (5) обеспечивают выполнение условий предшествования работ в соответствии с топологией сети: время начала выполнения каждой работы должно быть не меньше времени окончания непосредственно предшествующих ей работ, (6) — условие неотрицательности.
Если в последнее событие сети п входят сразу несколько работ, то необходимо добавить фиктивную работу (n, n+1), время выполнения которой равно нулю (ton,n+1-tнn,n+1=0 добавить в ограничение (4)). Тогда целевая функция запишется так
tкр=ton,n+1 → (min)
Приведенные постановки задачи относятся к классу задач математического программирования и могут быть решены известными методами в зависимости от вида функций fij (хij). Если предположить, что продолжительность выполнения работ линейно зависит от дополнительно вложенных средств и выражается соотношением

где kij — технологические коэффициенты использования дополнительных средств, то будем иметь задачу линейного программирования.
Пример.
Для сокращения срока реализации проекта, представленного сетевым графиком (рис.10), заказчик выделил 14 ед. дополнительных средств. Продолжительность выполнения работ линейно зависит от дополнительно вложенных средств и выражается соотношением t'ij = tij - kij xij. Известно, что kl2=0,1; k13 = 0,2; k23 = 0,5; k24 = 0,3; k35 = 0,6; k45 = 0,1. Над каждой работой поставлена ее продолжительность tij и минимально возможное время выполнения dij.
 Рис. 10
Рис. 10
Требуется оптимизировать сетевой график по времени, то есть найти такие  ,
,  , xij чтобы:
, xij чтобы:
а) время выполнения всего проекта было минимальным;
б) сумма дополнительно вложенных средств не превышала 14 ед.;
Ниже приводится образец решения задачи в Excel
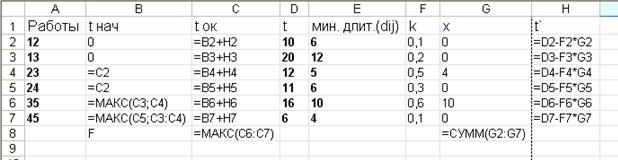


Таким образом, при дополнительном вложении 14 ед. комплекс работ может быть выполнен за 30 ед. времени. При этом средства распределятся следующим образом: 4 ед. в работу (2, 3) и 10 ед. в работу (3, 5) (Рис.4).
Постановка задачи 2. Пусть задан срок выполнения проекта to, а расчетное tкр > to. В этом случае оптимизация комплекса работ сводится к сокращению продолжительности критического пути. Задача заключается в определении величины дополнительных вложений xij в отдельные работы проекта, с тем чтобы общий срок его выполнения не превышал заданной величины to, а суммарный расход дополнительных средств был минимальным. Время выполнения каждой работы должно быть не меньше минимально возможного времени dij.
Математическая запись этой задачи:
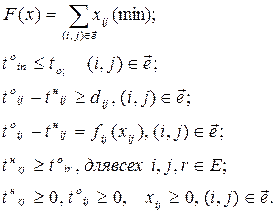
Смысл ограничений аналогичен соответствующим ограничениям постановки задачи 1 (1) — (6).
Приведенные постановки задачи относятся к классу задач математического программирования и могут быть решены известными методами в зависимости от вида функций fij (хij). Если предположить, что продолжительность выполнения работ линейно зависит от дополнительно вложенных средств и выражается соотношением

где kij — технологические коэффициенты использования дополнительных средств, то будем иметь задачу линейного программирования.
Не нашли, что искали? Воспользуйтесь поиском: